Limits of Predictability in Human Mobility

• Authors: Chaoming Song, Zehui Qu, Nicholas Blumm, Albert-László Barabási
• Publication, Year: Science, 2010
• Link to Paper

Overall Findings

• The authors utilize cellphone data to measure the limit to which you can predict human movement.

• They find that, despite the seemingly random movement of people across the world, people are extremely predictable and at any given time they typically will be in 1 or 2 locations (assumed to be home and work)

• They also find that those who travel further distances on a regular basis are more predictable which they consider to be surprising.

  • To me, however, this seems expected (see My Own Thoughts for more on why I think this)

Introduction

• Current models of human activity are fundamentally stochastic

  • Why?
  • For an individual looking at their own schedule, it seems far from random
  • However, for anyone else, the events seem quite random. Building on this idea, many models fall back on this concept that on average we moved through the world randomly

Our goal here is to quantify the interplay between the regular and thus predictable and the random and thus unforeseeable, probing through human mobility the fundamental limits that characterize the predictability of human dynamics.

• (These are very broad conclusions about human behavior from cell phone data. This seems a bit overstated.)

Data

• Mobile phone records collected by a phone company

• 3 months of data

• 50,000 cell phone users, selected from ~10 million users

  • Criteria for selection:

    • Visit more than two locations during the observed time period

    • Average call frequency $f$ is $\ge 0.5 \text{ hour}^{-1}$

      • See supplementary details for more explanation

• Phone carriers record the location of the closest cell tower when he phone is utilized, from this they estimate a users geographical location

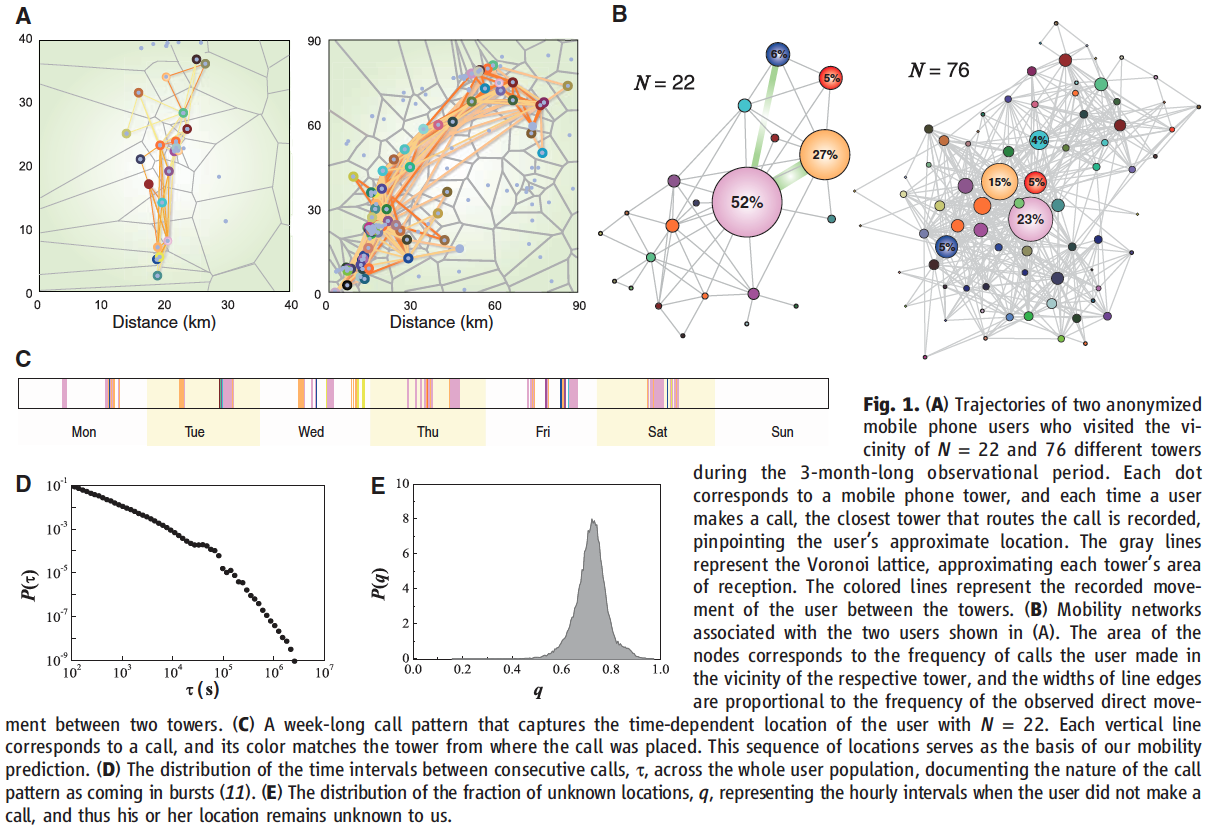
• Fig 1 A, distinct travel maps of users travel to $N = 22$ towers within an ~30-km range and another which travels to $N = 76$ different towers in an ~90-km range

• Fib 1B, the amount of time that a user spent in each region correlates with the size of the node in the network

• Fig 1C, captures the temporal sequence of towers visited

Entropy

Entropy is probably the most fundamental quantity of capturing the degree of predictability characterizing a time series.

• They create three different measure of entropy, capturing three different aspects of the information that they've gathered from their data set

  1. Random entropy —> $S_{I}^{rand} \equiv log_2N_i$

     • where $N_i$ is the number of distinct locations visited by​ user $i$
     • captures the degree of predictability of the user's whereabouts if each location is visited with equal probability (i.e. randomly)

  2. Temporal-uncorrelated entropy —> $S_{I}^{unc} \equiv -\sum_{j=1}^{N}p_i(j)\text{ log}_2p_i(j)$

     • where $p_i(j)$ is the historical probability that location $j$ was visited by the user $i$
     • characterizing the heterogeneity of visitation patterns

  3. Actual Entropy —> $S_i$

     • Depends not only on the frequency of visitation, but also the order in which the nodes were visited and the time spent at each location
     • This captures the full spatiotemporal order present in a person's mobility pattern
  • Naturally, for each user, $S_i \le S_{I}^{unc} \le S_{I}^{rand}$

• Fig 1D, users tended to place most of their calls in short bursts, followed by long periods with no call activity — during which they have no information about the user's location — Fig 1C

• Incompleteness of the data is represented by the variable $q$ (see Fig 1E)

  • Fig 1E shows us that a large portion of the data displayed was missing a lot of data
  • However, they found they could predict outmodes well with a $q$ value less than 0.8
  • Thus, they removed all of the data with a $q$ value higher than .8 (5000 users - 45,000 users remained)

• Then they calculated all measures of entropy.

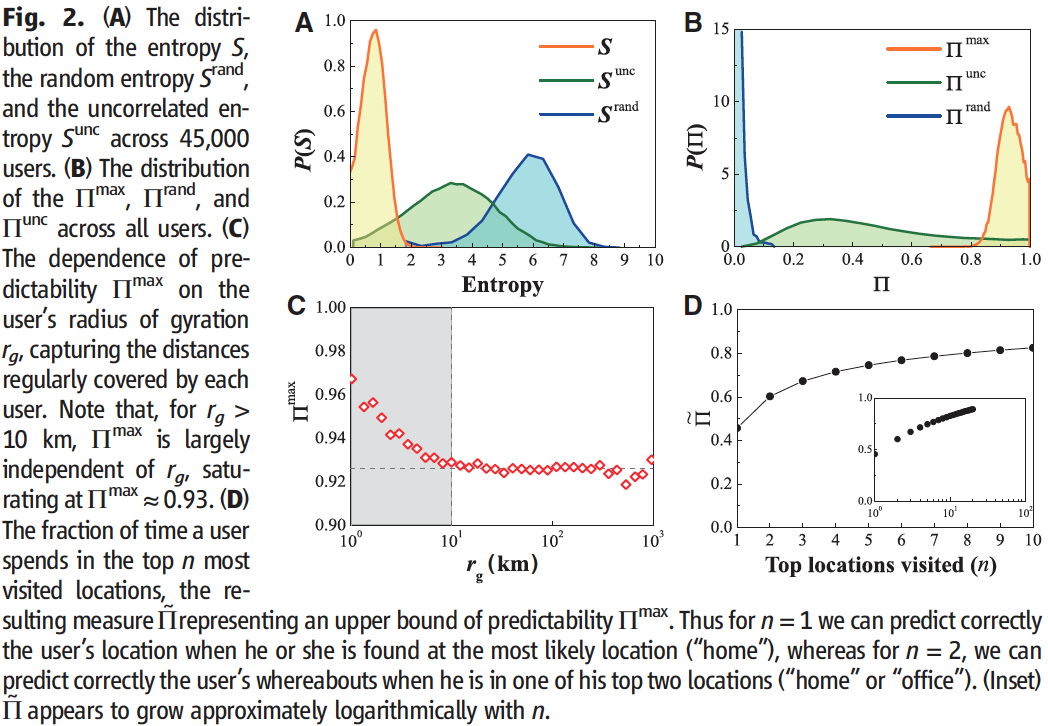
• Fig 2A

  • Find a stark difference between pure entropy and random entropy

    • Random entropy peaks at $S^{rand} = 6$ (bits of information)

      • This suggests that a user who chooses their next location at random can be found at any of $2^{S^{rand}} \approx 64$ location

    • Pure entropy peaks at $S = 0.8$ which suggests that the real uncertainty in a typical user's whereabouts is not 64 but $2^{0.8} = 1.74$, i.e. fewer than two locations

• Fig 2B

  • $\Pi^{max} =$ The fundamental limit of each individual's predictability (how predictable they are)

    • $\Pi^{rand} =$ Predictability based on random decisions
    • $\Pi^{unc} =$ Predictability based on only temporal/sequential information

  • $P(\Pi^{max})$ Was found to narrowly peak at $\approx 0.93$ —> this means that we can predict with 93 % accuracy the future whereabouts of a user

  • This indicates that, despite the randomness of individual movement, we typically move in extremely predictable patterns

• Fig 2C

  • Shows that $\Pi^{max}$ is independent from $r_g$ (travel distance) once that distance is greater than 10kms
  • Thus, individuals who regularly travel $\ge 100$kms are no less predictable than users who travel $\approx{}$ 10kms regularly

Understanding this degree of predictability

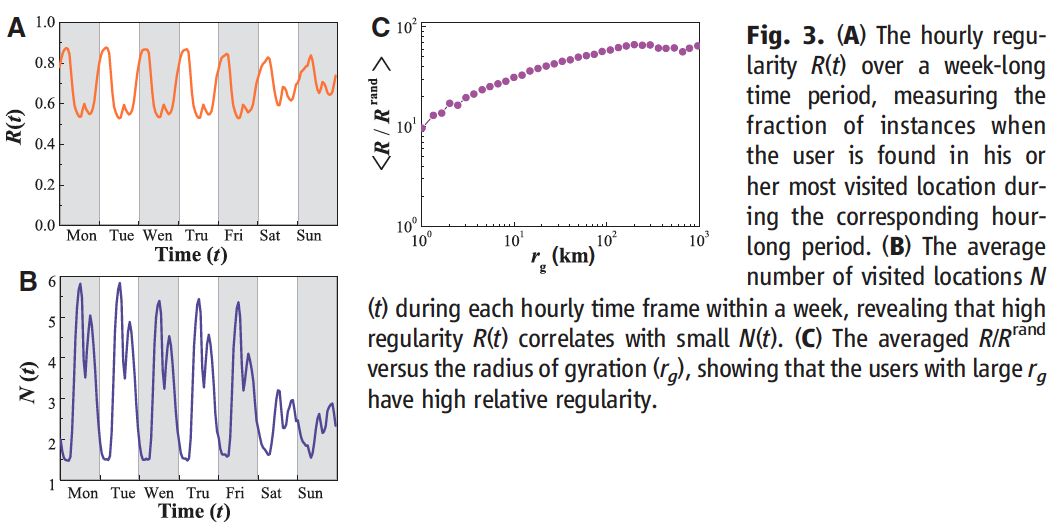
• To nail down what was going on here, they broken the data down into $24 \times 7 = 168$ hourly intervals and then identified the most visited location, within that hour

• A users Regularity $R =$ probability of finding the user in his/her most visited location during that hour

  • Represents a lower bound on predictability, because it does not include the temporal information

• Fig 3A & B

  • $R \approx 0.7$ across the entire dataset

    • This means that, on average, 70% of the time the most visited location coincides with the user's actual location

  • This measure $R$ is time dependent, however...

    • At night $R \approx 0.9$ (as individuals are likely home asleep)
    • Between noon and 1pm, and 6pm and 7pm, $R$ displays a clear minima (as people are traveling for lunch/dinner/commute)

  • We can see comparing A and B below, that ...

    • High regularity $R(t)$ correlates with low number of total distinct locations $N(t)$

  • Fig 3C shows us that users with a larger travel radius $r_g$ actually have a higher level of relative predictability

My Own Thoughts

In this paper the authors often seem surprised by the fact that an increased travel distance does not translate into a decreased predictability. However, to me this is exactly what I would expect.

People only travel large distances on a regular basis if they are doing so for their work. While some people certainly do travel long distances for other reasons, these typically would constitute traveling for holiday's and/or vacation, which would also be relatively predictable and, furthermore, relatively rare over a long enough temporal period.

Thus, if you accept this premise, their finding that those who travel further distances are more predictable makes perfect sense because, the unpredictability of an individuals movement seems to derive from when they are traveling for things other than work. If you are traveling two hours one way to work every day — you don't have the time, energy, or the desire to inject unpredictable movement into your everyday life.

People who do not travel far for work have more time to do spontaneous things and, thus, have more opportunity to increase the degree to which they can move randomly throughout the world.

Notes by Matthew R. DeVerna