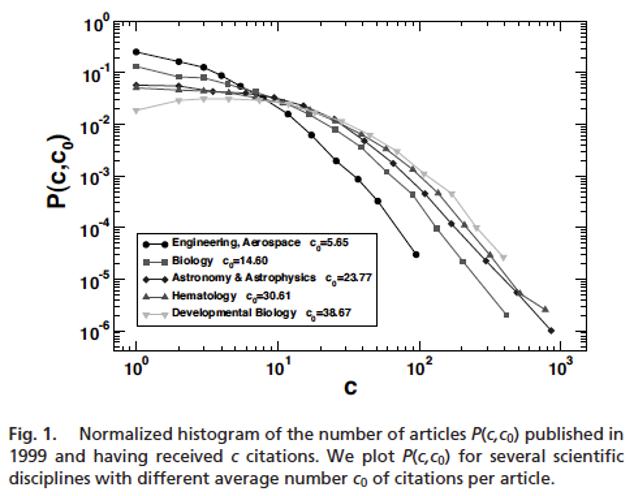

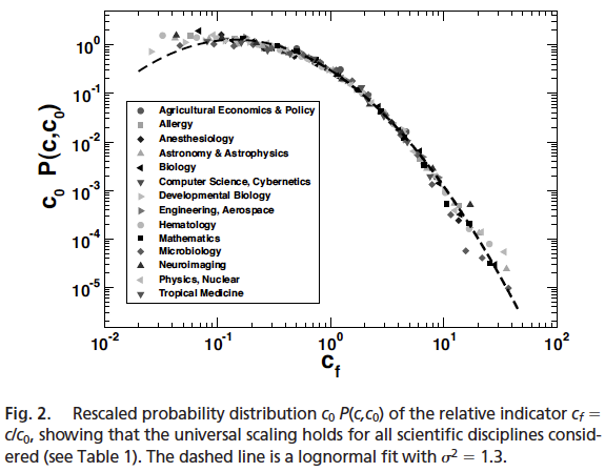
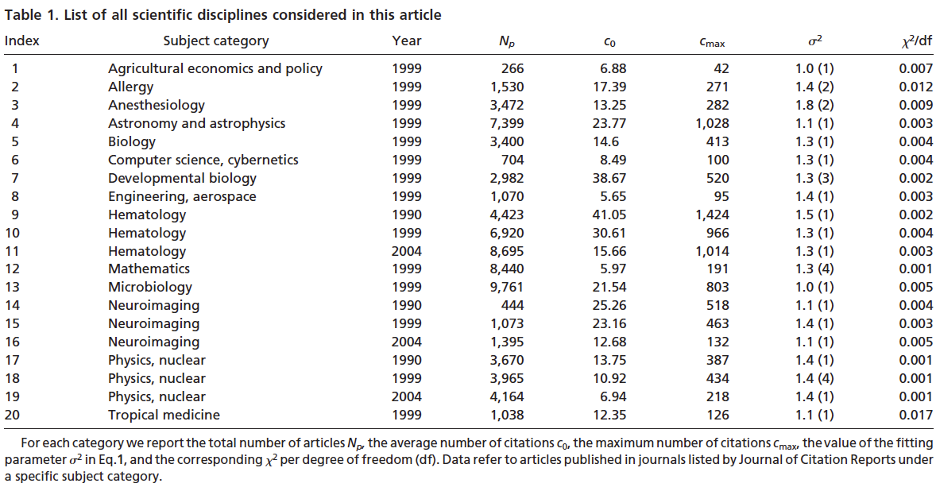
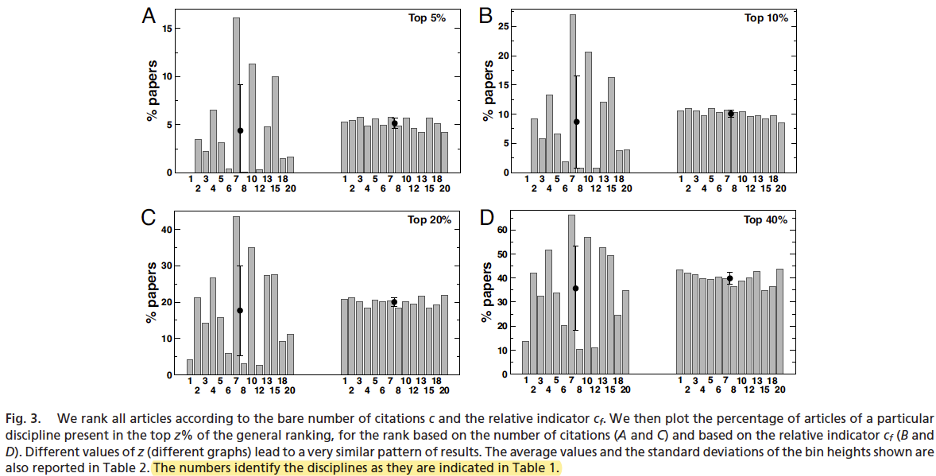
...the simple count of the number of citations is patently misleading to assess whether a article in Developmental Biology is more successful than on in Aerospace Engineering
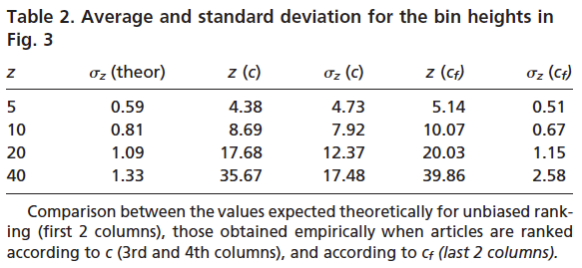
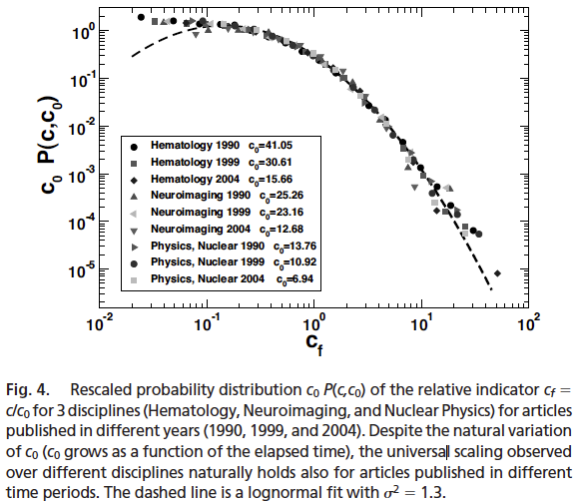
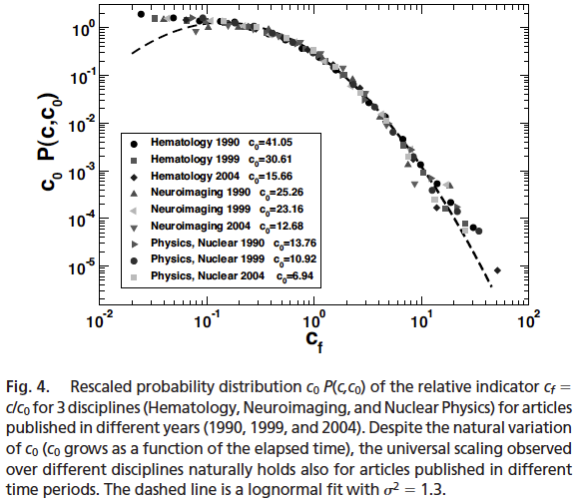
| Rank () | Avg. Pubs. () | Reduced Rank () | Keep Going? () | |
|---|---|---|---|---|
| 4.1 | 1 | 2 | .5 | Yes |
| 2.8 | 2 | 2 | 1 | Yes |
| 2.2 | 3 | 2 | 1.5 | Yes |
| 1.6 | 4 | 2 | 2 | No |
| .8 | 5 | 2 | ||
| .4 | 6 | 2 |