Searching for superspreaders of information in real-world social media

• Authors: Sen Pei, Lev Muchnik, José S. Andrade Jr., Zhiming Zheng, & Hernáan A. Makse
• Publication, Year: Scientific Reports, 2014
• Link to Paper

Overview and Major Findings

• Utilizing real-world social network data, the authors compare the performance of common topological measures in order to identify the best way to locate the most influential users within a network.

• Metrics compared:

  1. k-core/k-shell: see the wikipedia page for a quick crash course or this paper for more details.
  2. PageRank: Wikipedia for details
  3. Degree: the degree of a node in a network is the number of connections it has to other nodes. Wikipedia for details

• Networks examined:

  1. LiveJournal.com connections
  2. Scientific publishing in American Physical Society (APS)
  3. Twitter mention networks
  4. Facebook friend/post networks from a regional network corresponding to the city of New Orleans, LA, USA

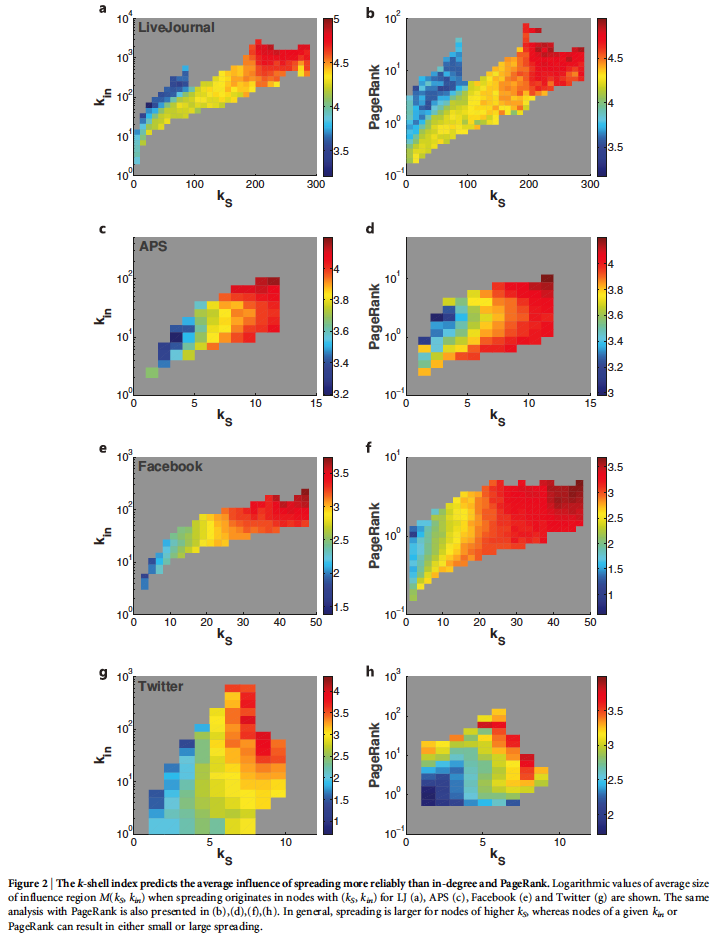
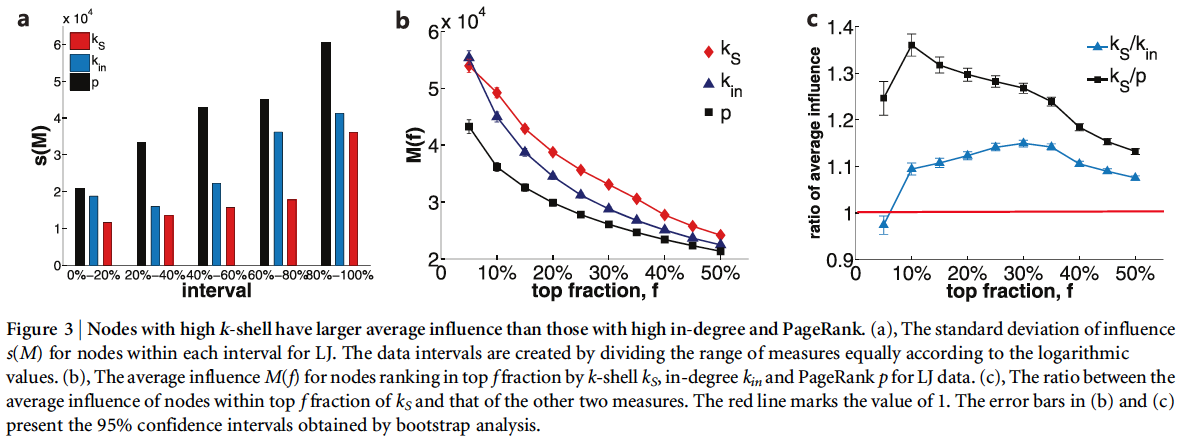
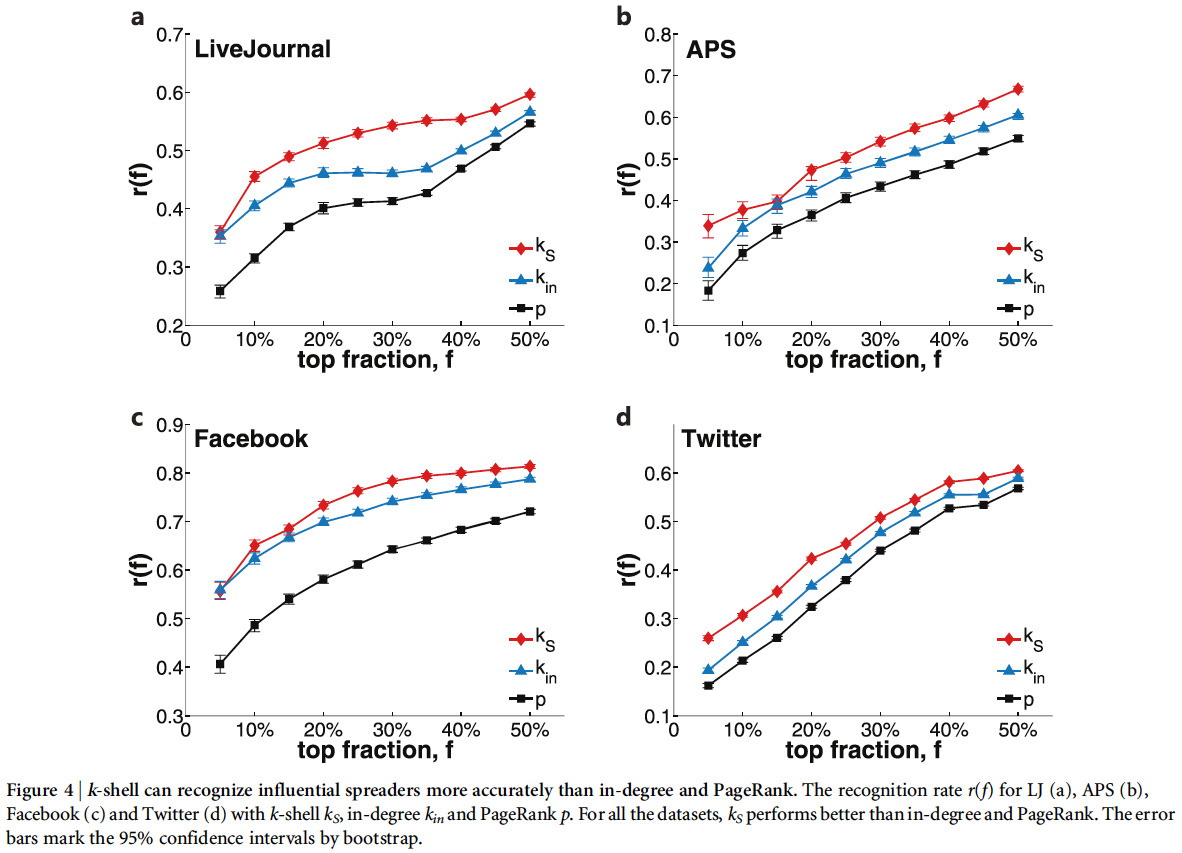
• For all of these networks they show that k-core does the best job of identifying superspreaders of information

• They also develop a "local proxy for influence" which appears to perform similarly to k-core — the sum of the nearest neighbors' degree

Background

• Central motivation for this research: previous work seeking to develop methods for identifying superspreaders of information did not look at real-world data and instead rely on simulations based on models of infection and or rumor spreading such as SIR.

  • As a result, they highlight numerous times that the conclusions within this work is model dependent and has led to conflicting results
  • Thus, they collected large real-world network data to test the methods most commonly utilized (PageRank, k-core, degree)

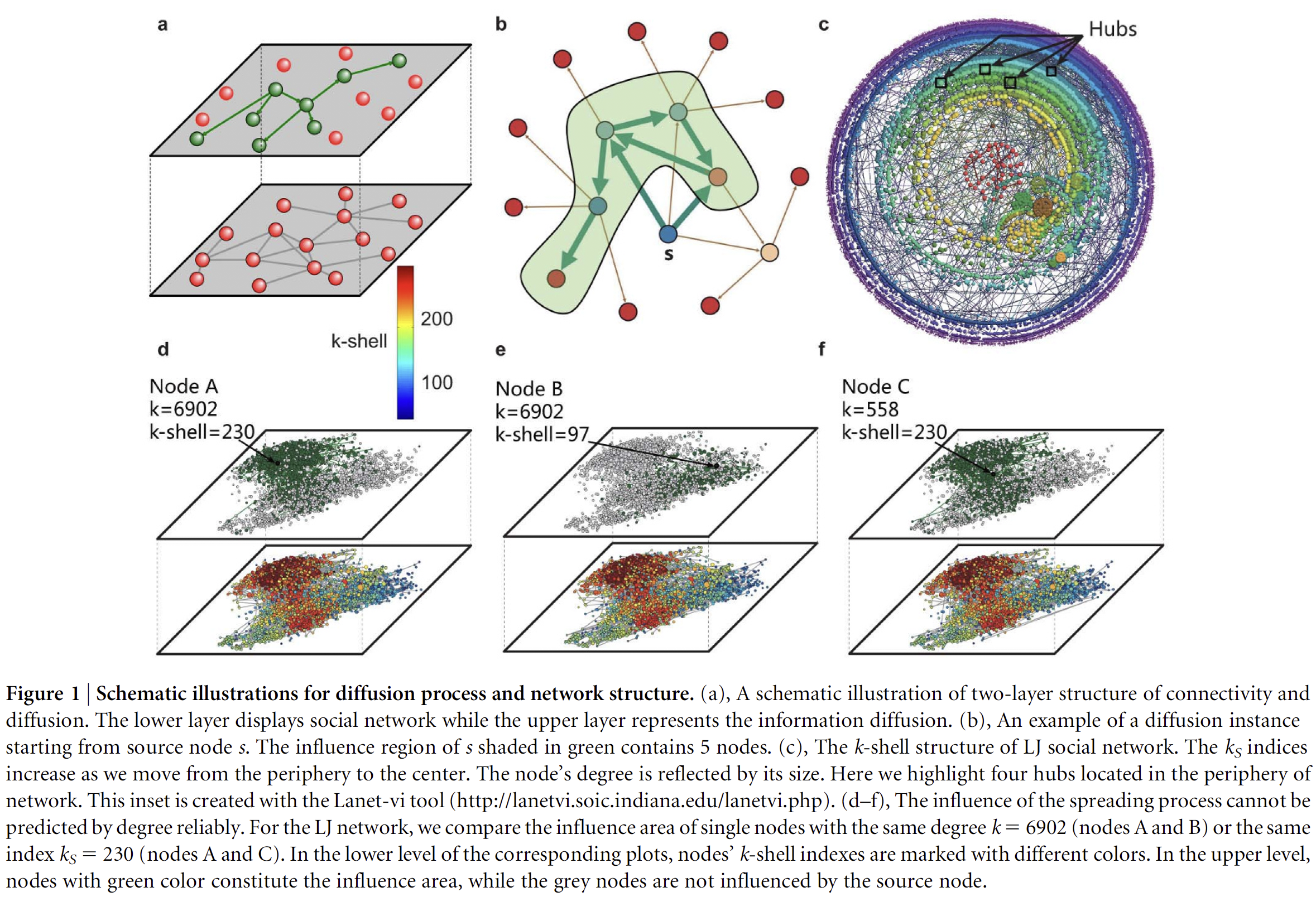
General approach taken in this study

• Essentially, what they then do is calculate the average influence and recognition rate for each of the three network topology metrics, for all of the different networks.

average influence

The average influence, $M(k_s, k_{in})$, is calculated for nodes with a given combination of $k_s$ (k-core) and $k_{in}$ (in-degree) as:

Where,

• $\Upsilon(k_s,k_{in})$ is the collection of all the users participating in a diffusion of information
• $N(k_s,k_{in})$ is the number of those users

recognition rate

The recognition rate is defined as

Where $I_f$ and $P_f$ are sets of nodes ranking in the top $f$ fraction by influence and predictor, respectively, and $|I_f|$ is the number of nodes in $I_f$ .

• So, basically what they do is:

  1. Create a ranked list of all nodes from highest to lowest influence.
  2. Figure out which nodes are identified as the most influential by a specific predictor (i.e., k-core, in-degree, or PageRank) above some specific fraction $f$
  3. Take the intersection of the top $f$ fraction of the influential list ($I_f$) and the predicted list $P_f$
  4. Take the number of nodes in this intersection and divide it by the total number of nodes within the top $f$ fraction of the most influential nodes

• Thus, if $I_f$ and $P_f$ were the exact same set of nodes, they $r(f)$ value would equal $1$.

Results

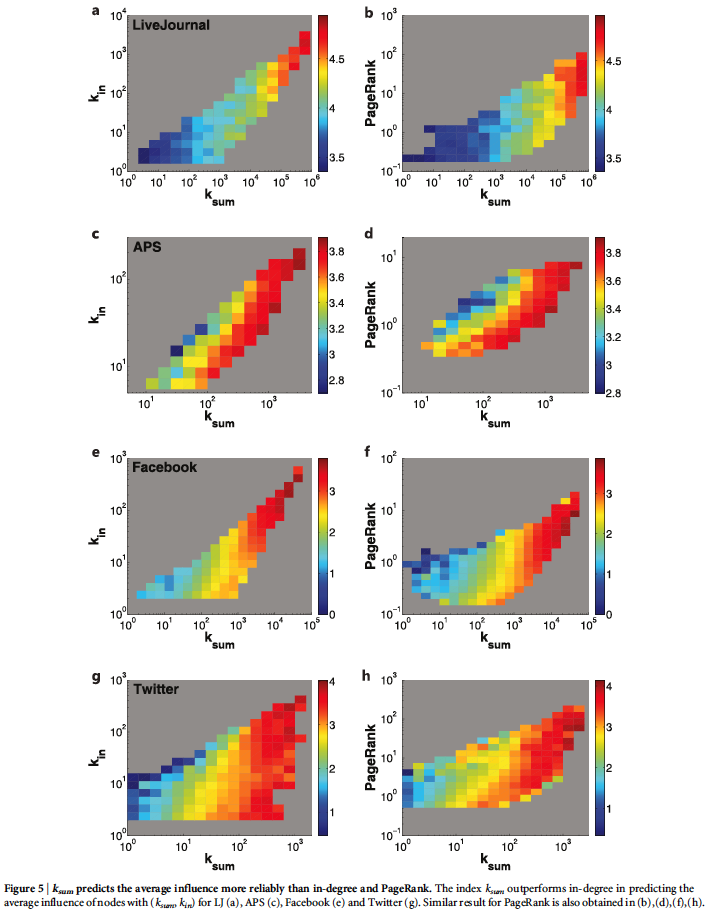
They illustrate a number of different ways that k-core does the best for all networks in pretty much all ways. I simply paste the figures and their descriptions below to illustrate the results.

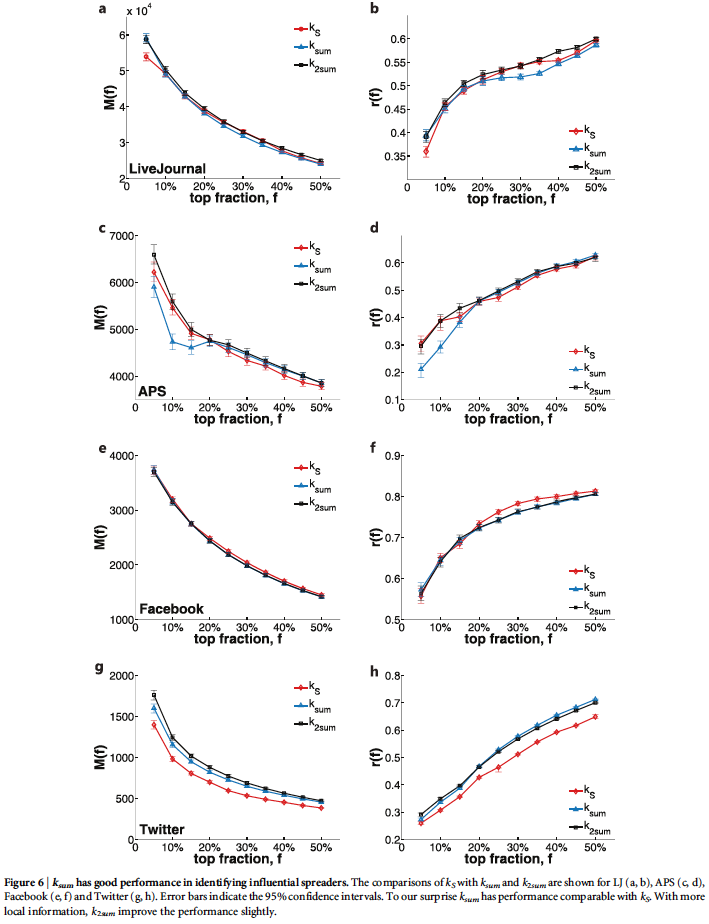
Local Proxy

Since k-core is a global measure it's usefulness is quite limited — rarely to we have a full picture of all the connections within a social network.

Thus, the authors offer a local proxy which seeks to stand in for k-core by utilizing only partial network information.

Because k-core appears to not only take into account the degree of an individual node but also the degree of those around it, the authors create and test two simple metrics:

1. $k_{sum}$ — Node $i$'s $k_{sum}$ is the sum of the degree of all the nearest neighbors of node $i$.
2. $k_{2sum}$ — Is the same as $k_{sum}$ except it now accounts for the nearest-neighbors of node $i$'s nearest neighbors. Thus, this measure takes the sum of node $i$'s nearest neighbor as well as the next nearest neighbor.

We can see below that $k_{sum}$ performs on-par with k-core and $k_{2sum}$ doesn't add much additional value.

Note: While this would certainly require much less Twitter data than reconstructing the entire network, gathering this data on just the nearest neighbors for even a small sample of Twitter users (say a few hundred) is still extremely temporally expensive and can require days to simply gather that data.