Complex Adaptive Systems: Computational Models of Social Life (Ch 5: pp. 57-77)

• Authors: John H. Miller, Scott E. Page
• Publication, Year: Princeton University Press, 2009
• Link to Book

Summary of Chapter

The authors generally address the idea of using computational techniques for theoretical purposes such as creation and/or testing. They address these ideas first from a someone philosophical perspective and then, in more detail, address (and largely refute) the specific objections to utilizing computational techniques for these purposes.

The general insights are:

1. As with any tool computational techniques must be utilized properly.
2. Computational techniques afford practitioners the benefit of more traditional techniques as well as additional benefits with respect to complex systems.

Computation as Theory

By the addition of such artificial Instruments and methods, there may be, in some manner, a reparation made for the mischiefs, and imperfection, mankind has drawn upon it self, by negligence, and intemperance, and a wilful and superstitious deserting the Prescripts and Rules of Nature, whereby every man, both from a deriv’d corruption, innate and born with him, and from his breeding and converse with men, Is very subject to slip into all sorts of errors.

— Robert Hooke, Micrographia

The use of computers seems thus not merely convenient, but absolutely essential for such experiments which involve following the games or contests through a very great number of moves or stages. I believe that the experience gained as a result of following the behavior of such processes will have a fundamental influence on whatever may ultimately generalize or perhaps even replace in mathematics our present exclusive immersion in the formal axiomatic method.

— Stanislaw Ulam, Adventures of a Mathematician

To build "sturdy" computational structures/models, the social sciences have lost a bit of the uniqueness that comes from truly novel and unique types of models.

As a result, this type of novelty is scarified. They begin the chapter by "suggesting that it is time to take our old components and use them in new ways. Such an approach is not without risks, for surely some of the new structures that we build will fall; but others will stand and inspire."

Theory vs. Tools

A theory is a cohesive set of testable propositions about a phenomenon, and it can be created by employing a variety of tools.

Mathematical models are tools often used in economics, however, there is no a priori reason to think that mathematical models are superior to any other type of tool for theory construction.

The reality is that different tools will help address different aspects of complex problems.

By attacking problems on numerous fronts, breaches in nature’s walls inevitably appear. Though it may be difficult to predict on which front the walls will first crumble, openings on one front are likely to lead to progress on another.

Physics Envy: A Pseudo-Freudian Analysis

In this section the authors, generally, are discussing the subtle differences in the ways in which physicists and economists approach problems. For example, they highlight that physicists may be more "casual" in their approach to a problem that ...

The premium in theoretical physics is on gaining insight into interesting phenomena. If the insight is there, then there is little desire for mathematical rigor. Consequently, in physics there is a sharp distinction between the mathematical and theoretical branches. Having a good insight and stating a theorem that is not rigorously proved is acceptable behavior.

Theory must result in insight and withstand testing.

Thus, in physics you can have a theorem that is widely accepted but not rigorously proved.

The benefit of this approaching problems without necessarily requiring axiomatic rigor is that it offers researchers an increased level of freedom to try and understand...

… nature's mysteries, and when it is exercised well, it can lead to significant advances.

Computation and Theory

Like all new tools that are brought into the scientific process, computational models confront a variety of universal concerns: Can these tools generate new and useful insights? How robust are they? What biases do they introduce into our theories? These concerns are obviously important for any type of tool we use in modeling (both traditional and new).

For any tool we employ, it is always important that we remember the relevant issues surrounding its appropriate use, regardless of its current level of acceptance.

Computation in Theory

First, it is useful to note that the use of a computer is neither a necessary nor a sufficient condition for us to consider a model as computational.

The authors wish to focus on "agent-based" modeling.

Modeling proceeds by deciding what simplifications to impose on the underlying entities and then, based on those abstractions, uncovering their implications.

Agent-based modeling can be described with a few principles

1. The entities of interest are abstracted into "agents" which can be defined and manipulated based on specific assumptions and constraints
2. These agents are then proceed to interact with one another based on these "rules" and assumptions

The agent-based object approach can be considered “bottom-up” in the sense that the behavior that we observe in the model is generated from the bottom of the system by the direct interactions of the entities that form the basis of the model. This contrasts with the “top-down” approach to modeling where we impose high-level rules on the system—for example, that the system will equilibrate or that all firms profit maximize—and then trace the implications of such conditions. Thus, in top-down modeling we abstract broadly over the entire behavior of the system, whereas in bottom-up modeling we focus our abstractions over the lower-level individual entities that make up the system.

Agent-based modeling is desirable because sometimes the reductionist perspective can fail when observing systems. We may know the specifics of every individual component of a system, but until we model how they interact with one another as a larger system then we may not truly understand the system. Thus, agent-based modeling seeks to understand how lower-level components/entities/agents interact with one another to produce the larger-scale behavior of the system as a whole.

… even if we can fully uncover the microfoundations of behavior—for example, acquire a complete specification of the psychological aspects of behavior or the probability of interaction—we may still not have a simple way to understand their macrolevel implications.

Computation as Theory

Good models tend to have a few properties:

1. Focus on simple entities and interactions
2. Implications tend to be robust to a diverse set of changes to the underlying structure of a system
3. Tend to produce "surprising" results that motivate new predictions
4. Can be communicated easily to others
5. Are useful in new applications and contexts

As the structure of a model becomes more complicated, many of these desirable features are lost, and we move away from modeling toward simulation.

Objections to Computation as Theory

While the notion that one can do productive theoretical work using computation models is becoming more widely accepted, it still seems to provoke intense objections by some researchers. Here we attempt to address some of the usual objections to computation as theory.

Computations Build in Their Results

A common objection to computation is that the answers are “builtin” to the model, and thus we can never learn anything new from these techniques. Clearly, the first part of this objection is absolutely correct—the results of the computation are built-in since the computer will, without error, follow its predetermined program. ¹ Nonetheless, the inference that somehow this makes computation an unacceptable theoretical tool is wrong.

The general idea here is that no matter what theoretical tool you're using, they have some sort of "built-in" answer.

• For example, if you ask a certain type of academic to produce and answer to question X , you will likely get relatively similar answers because their approaches will be similar.

The central concern should always be whether the tool you are using, whatever it may be, delivers a conclusion that is due to an unrealistic feature of that tool or it's ability to demonstrate/observe/simulate nature correctly.

Poorly done models, whether computational or mathematical, can always fail because their results are driven by some hidden or obscure black-box feature. Having a premium on clarity and scientific honesty about what is driving the results will always be needed regardless of the theoretical medium.

To create models that go beyond our initial understanding, we need to incorporate frameworks for emergence. That is, we need to have the underlying elements of the model flexible enough so that new, unanticipated features naturally arise within the model.

By way of an analogy, consider giving students some clay and telling them either to make a coffee mug or an object suitable for drinking a liquid. In both cases, the underlying material (clay) is very flexible, but depending on the instructions we issue we may get very different objects. The instructions to “make a coffee mug” are likely to lead to a set of very similar objects, whereas the request to “make an object suitable for drinking a liquid” could result in a host of possibilities. Useful models arise when we impose just enough instructions to get objects of interest, but not so many as to preimpose a solution.

Computations Lack Discipline

Another common objection to computational models is that they lack sufficient discipline or rigor to be of use.

This is dumb. Obviously, any tool can be used incorrectly. Like any other tool, computational models must be employed rigorously.

The flexibility of creative freedom allowed by computational models can sometimes seduce practitioners to endlessly tinker and insert features within their models — this practice must be moderated if a reliable model is to be developed.

The inherent flexibility of computational models can also make them hard to understand and verify.

The newness of computational models means that a rigorous set of standards are not as concretely employed as mathematical models. However, some standards are being developed and, as with any tool, good practice is the responsibility of the practitioner.

The fact that computational models are convenient and flexible should be viewed as a distinct advantage.

These new tools allow us to address problems that were previously unaddressable. The application of such computational tools may then yield problems which can be addressed with more traditional methods.

Computational Models Are Only Approximations to Specific Circumstances

Computational models often result in answers that may be approximations that cannot be directly verified as being correct. Relying on such approximations may be perfectly acceptable, given the potential high cost of getting exact solutions, and even necessary in those cases where exact solutions are infeasible. Moreover, there are techniques, both in how models are formulated and how they are tested, that should help ensure that the results we are finding are not due to some computational anomaly.

Another limitation is that computational models may be less generalizable than traditional models. For example, they often need to be rerun given a new set of circumstances

• This process can be automated but it still comes with some level of cost

That being said, the ability to use a traditional model in a generalizable way is more a result of how that model was constructed, and is not necessarily inherent to any traditional model.

Computational Models Are Brittle

Computational models are often thought to be brittle, in the sense that slight changes in one area can dramatically alter their results.

The authors point out, however, that this is shared for more traditional mathematical models when the form of certain parameters is change — i.e. "the form of the utility function or the compactness of the strategy space"

For good modeling we need to keep in mind the brittleness of our tools and actively work to avoid producing theories that are too closely tied to any particular assumption.

• This will be true for any and all tools utilized by a researcher

Brittleness in computational models can be prevented by:

• Having a simple and obvious design

• Utilizing emergence frameworks

• Creating sets of alternative implementations for key features of the model

  • For example, models that focus on adaptive agents can implement different types of adaptive algorithms

• Other techniques, such as employing Active Nonlinear Testing (ANTs) can be utilized (Fig. 5.2)

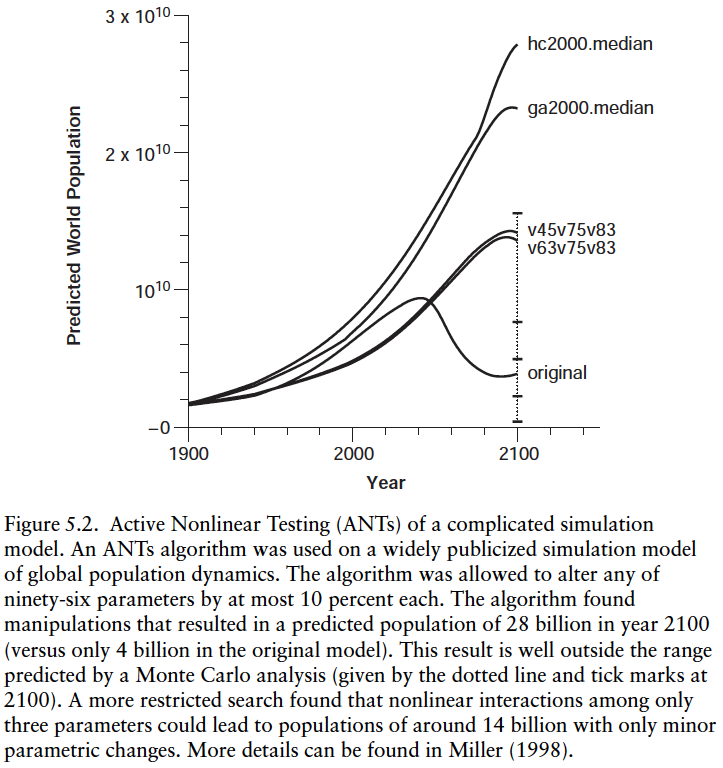
As more and more computational models are developed and explored, our understanding of the typical areas where brittleness may occur will be improved. Such an understanding will not only help us create better models, but it should also be of use in furthering our understanding and control of real systems.

Computational Models Are Hard to Test

Although complex systems and equilibrium models can differ in how they produce testable hypotheses, overall what they produce is quite similar. In both cases we can make refutable predictions.

Equilibrium models like that of supply and demand can lead to specific predictions which can be tested upon based on real world data. However, complex systems are very sensitive to their initial states and often include positive feedback loops which can create large differences in predictions.

For these types of systems, as well as those which can be represented with more standard models, computational models still provide testable outcomes. That being said, typically we are comparing a much larger distribution of outcomes as opposed to a collection of single point predictions.

• This may actually allows us to make more testable predictions because we can begin to address how the variance of specific parameters may affect outcomes.

Even as purely abstract objects, computational models are useful. They provide an “artificial” reality in which researchers can experience new worlds in new ways. Such experiences excite the mind and lead to the development of novel and interesting ideas that result in new scientific advances.

Computational Models Are Hard to Understand

Finally, computational models are often dismissed because it may be difficult to fully understand the structure of the model and the various routines that drive it. Regardless of how the models are communicated, it is always easier to describe and understand simpler models. The actual computer code itself is a complete specification of the model, but there is a big difference between a complete specification and an accessible one. Indeed, most computer programmers have had the experience of looking at someone else’s code (or even their own) and not being able to decipher it without a very intensive analysis.

• Part of the issue is a lack of standardization with respect to coding practices and the communication of computational models

  • The authors mention the Unified Modeling Language (UML) as a potential solution (though this reader has not yet heard of it or seen it implemented)

Ultimately, computational modelers must strive to create simple, easily communicated models. … Core propositions in computational models are surrounded by lines of computer codes; in mathematical models, such propositions are surrounded by various solution techniques arising from, say, the calculus or linear algebra. In either case, it is the core propositions that we need to focus on and communicate.

New Directions

A lot of this section is spent discussing the types of models that the authors plan to address in future chapters of the book. Mainly, they are interested in agent-based models, suggesting they offer specific advantages with respect to complex systems.

Notes by Matthew R. DeVerna