Complex Adaptive Systems: Computational Models of Social Life (Ch3: pp. 35-43)

• Authors: John H. Miller, Scott E. Page
• Publication, Year: Princeton University Press, 2009
• Link to Book

Modeling

For every Complex problem, there is a solution that is simple, neat and wrong.

— H. L. Mencken

Things should be made as simple as possible — but no simpler.

— Albert Einstein

Nothing is built on stone; all is built in sand. But we must build as if the sand were stone.

— Jorge Luis Borges

Models as Maps

• One of the best models that we encounter in our daily experience is the road map.

• Maps are valuable for a variety of reasons

  • They leave out a lot of unnecessary details

    • This minimizes distractions and allow us to focus on the questions that are most important to the user

    • Adding more and more details moves us closer to reality and can obfuscate the benefit of ever creating the map

      • e.g. an exact, to-scale size map of a city would necessarily be the size of the city and, thus, unusable

  • They are easily understandable to others

    • This often requires that there is some sort of implicit understanding on the part of the user

      • For example, map users implicitly understand that, more often than not, the shortest way from point A to point B is not a straight line (e.g. the straight line may go through a rough mountain terrain, while taking the highway around would be much faster)
      • Misunderstandings about implicit knowledge embodied in a map can often lead to serious mistakes

  • They allow us to predict key features of the world, but they also enable us to discover new phenomena

    • A map of the world may give rise to the theory of continent drift

    • Plotting earthquakes locations could be used to find hidden fault systems

    • Snow's 1885 map of cholera cases in the Soho district of London revealed both the mode of transmission and source (a pump on Broad Street) of the disease

      • None of these phenomena were anticipated by the original map makers who were focused solely on the accurate representation of the real world in a compact form

A More Formal Approach to Modeling

• The top half of the picture represents the real world, the bottom represents the model

  • This framework is based largely on Holland et al. (1986) modeling ideas for creating artificial learning systems

Breaking Down the Formal Model

• We assume that the real world consists of various states $S$

• A transition function $F(S)$ exists which maps a given state at time $t$ into a new state at time $t + 1$

  • $F(S)$ is unknown but is what the modeler hopes to uncover

    • Discovering the exact transition function is likely impossible due to the high dimensionality of the problem (for example, think of predicting the weather) creates a state space which is simply too large to account for (theoretically, for weather prediction, all relevant atoms)

• To reduce the state space a modeler generates equivalence classes (designated $E(S)$)

  • These equivalence classes map real-world states ($S$) to a model state ($s$)
  • Utilizing the weather prediction example, making relevant configurations of atoms into measures of barometric pressure and humidity would represent equivalence classes in this example

• Once equivalence classes have been generated, we then need to find a transition function for our model, $f(s)$, that can predict how patterns of pressure and humidity are transformed over time

The success of a particular mode is tied to its ability to capture the behavior of the real world.

• If we end up in at the same model state regardless of whether we...

  1. First transform the initial real-world state into its equivalence class and then run it through the model's transition function, or
  2. First allow the real-world state to be transitioned to its next state and then map this state, via the equivalence class, to the model

• … the model coincides with the world.

Put another way (equations)...

• If we start with real-world state $S'$

• The model transforms this state into $s' = E(S)$

  • Then predicts that we end up at $f(s')$ in the next time period

• While the real-world state becomes state $F(S')$ in the next time period

The model "coincides" with the real world if

The requirement that the maps between the model and the real world must be commutative in this way is known as a homomorphism. Thus, the goal of modeling under this view is to find a set of equivalence classes and a transition function that results in a useful homomorphism.

A model requires choices of both the equivalence classes and the transition function, and the art of modeling lies in judicious choices of both.

• There are likely many difference equivalence mappings (and associated transition functions) the value of any particular set of choices depends on the current need(s) of the modeler

• Choosing a broad set of equivalence classes makes finding the transition function simpler, but loses resolution and value

• Finding useful homomorphisms is often difficult in practice

  • Modelers may be willing to forgo perfect homomorphism because even non-perfect models can be very useful, despite outlier/exceptions to the model
  • However, when the number of exceptions to the model becomes too great — the model should be updated/changed

This continual chasing of the "ideal" model results in a Schumperterian cycle of scientific creative destruction. Modelers attempt to reduce the world to a fundamental set of elements (equivalence classes) and laws (transition functions), and on this basis they hope to better understand and predict key aspects of the world. The ever present quest for refining old, and discovering new, ways to represent the world drives the process of scientific creative destruction.

Modeling Complex Systems

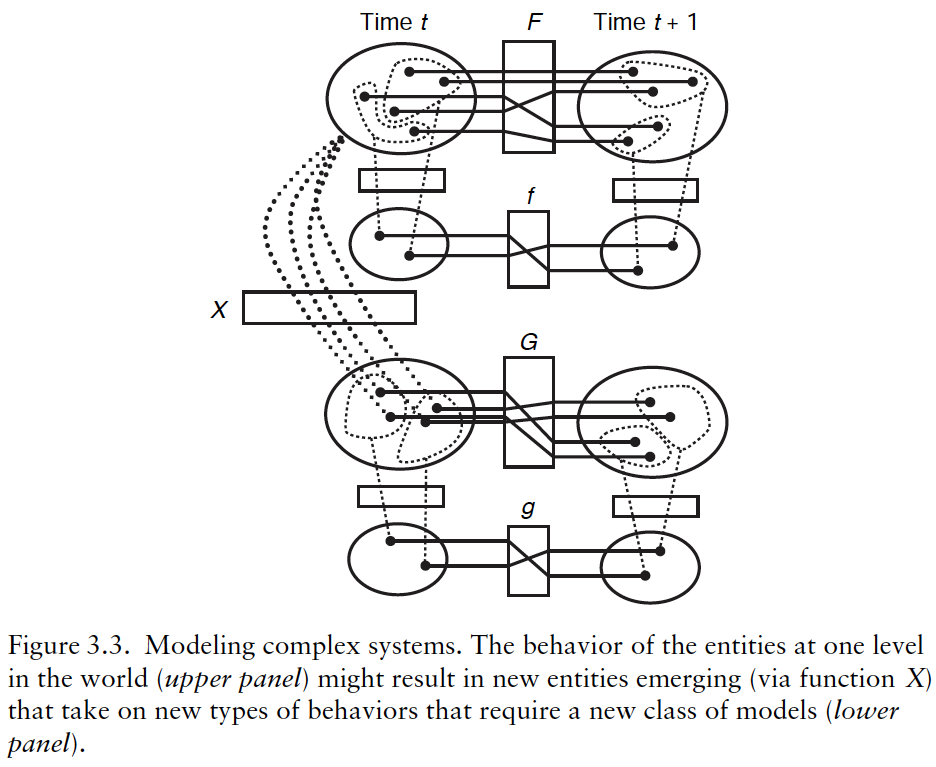
• Complex systems give rise to emergent behavior or properties

• To model this, we take the model from the previous section (Figure 3.2) and add an addition section, to represent new emerging entities and/or behavior (brought on by transformation function $X$ )

• In the social sciences, the two systems might be psychology and economics

  • Individual choice behavior in the low-level psychological system could aggregate into a very different homo economicus or firm entity in the higher-level economic system (via the unknown transformation function $X$)

• In the higher level world, higher-level entities are governed by a new transition function $G$

  • As in the lower-level system, we can model the interactions as shown in the bottom part of Figure 3.3
  • Note, however, that knowledge of the lower-level system does not help us model the new, higher-level system

• This idea that the higher level is completely unknown to us coincides with the idea of "hierarchical reductionism" put forth by Dawkins (1976)

Each time we move to a new level, we are confronted with a new world that requires new models. Moreover, creating a theory about how these new levels arise from existing ones, namely understanding the function $X$, becomes important. We would like to be able to develop a theory that helps us understand how states of the world (composed of lower-level entities and interaction rules) are transformed into higher-level entities.

Modeling Modeling

Regardless of the system or methodology, our goal is to employ high quality models. Thus, we apply the same standards of simplicity and elegance to our computational models that we do to our mathematical ones. Models need to be judged by what they eliminate as much as by what they include—like stone carving, the art is in removing what you do not need. Even though a computational model may require thousands of lines of code, if done well it can still embody the simplicity and elegance that is demonstrated in a mathematical model existing in only a few equations.

Having an explicit awareness of the issues surrounding quality modeling is important if we want to work on the frontiers of science. This awareness disciplines our efforts as we explore new problems and employ novel techniques. Creating a model is much like trying to solve a brain teaser. Finding such solutions is often an extremely difficult task involving a combination of theory, practice, and a bit of art. Yet, once discovered, the answer has strong intuitive appeal and appears all too obvious.

Notes by Matthew R. DeVerna