Identification of influential spreaders in complex networks

• Authors: Maksim Kitsak, Lazaros K. Gallos, Shlomo Havlin, Fredrik Liljeros, Lev Muchnik, H. Eugene Stanley, and Hernán A. Makse
• Publication, Year: Nature Physics, 2010
• Link to Article

Summary

• The most highly connected individuals within a network are not always the most influential within that network
• The most efficient spreaders are those located within the core of the network, as identified by a k—shell decomposition analysis
• When multiple spreaders are considered simultaneously, the distance between them becomes the most crucial parameter in determining the extent of spread
• Infections persist in the high-k shells in the case where recovered individuals do not develop immunity

Introduction

• It was often believed that the most connected people (hubs) are the key players, responsible for the largest scale of the spreading process.
• In the context of social network theory, the importance of a node in the spreading process is often associated with the betweenness centrality, a measure of how many shortest paths cross through this node, which is believed to determine who has more `interpersonal influence' on others

Argument

"Here we argue that the topology of the network organization plays an important role such that there are plausible circumstances under which the highly connected nodes or the highest-betweenness nodes have little effect on the range of a given spreading process. For example, if a hub exists at the end of a branch at the periphery of a network, it will have a minimal impact in the spreading process through the core of the network, whereas a less connected person who is strategically placed in the core of the network will have a significant effect that leads to dissemination through a large fraction of the population."

General Approach

• Calculate -core ($k_S$) see Fig. 1, degree (k), and betweenness centrality ($C_B$), on number of real-world networks. The networks utilized are:

  1. Friendship network between 3.4 million members of the LiveJournal.com community
  2. Network of email contacts in the Computer Science Department of University College London
  3. Contact network of inpatients (CNI) collected from hospitals in Sweden
  4. Network of actors who have costarred in movies labelled by imdb.com as adult

• Utilize the SIR and SIS epidemic models to estimate influence of different nodes

When hubs may not be good spreaders

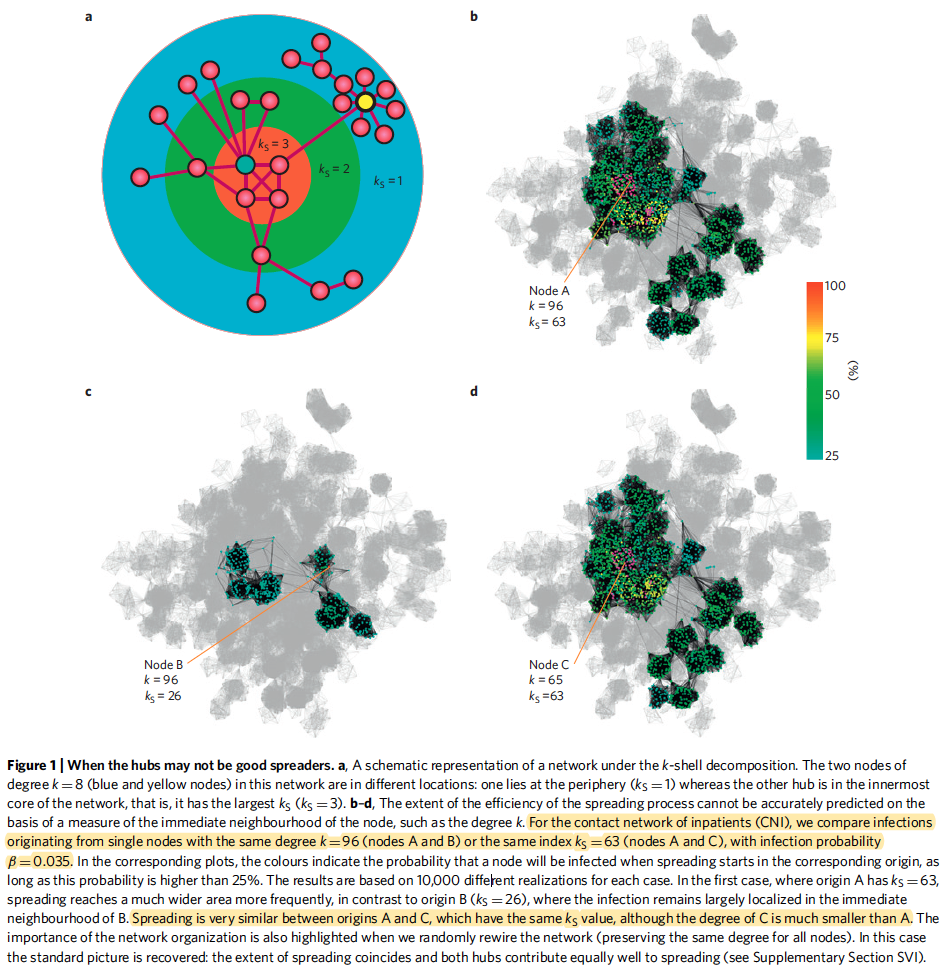
• The size of the population infected in a spreading process is not necessarily related the degree of the node (k) where the spreading started

  • Spreading may be different even when starting from nodes of similar degree (Fig. 1 b—d)

• Location of the spreading origin, given by $k_S{}$ predicts more accurately the size of the infected population (Fig. 1 b—d)

k-shell predicts spreading

"To quantify the influence of a given node $i$ in an SIR spreading process we study the average size of the population Mi infected in an epidemic originating at node $i$ with a given ($k_S$,$k$). The infected population is averaged over all the origins with the same ($k_S$,$k$) values:

$$M(k_S,k) = \sum_{i \epsilon\Upsilon(k_S,k)} \frac{M_i}{N(k_S,k)}$$

where $\Upsilon(k_S,k)$, is the union of all $N(k_S,k)$ nodes with $(k_S,k)$ values."

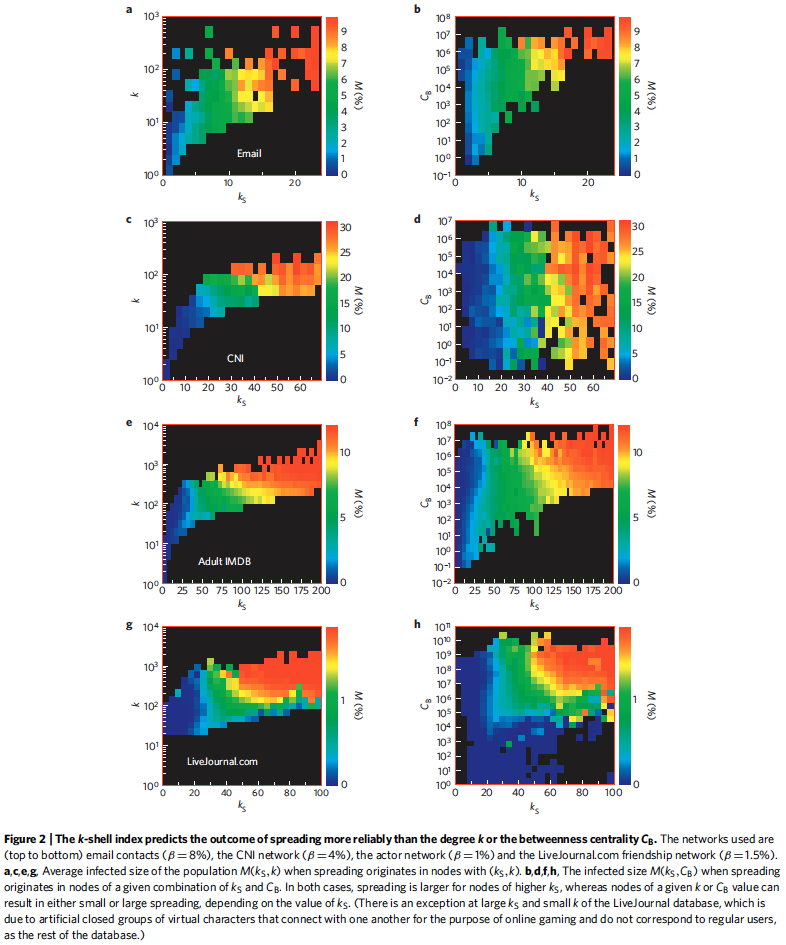
Studying $M(k_S,k)$ lead to three general results (illustrated in Fig. 2 (a,c,e,g))

1. For a fixed degree, there is a wide spread of $M(k_S,k)$ values.

   1. Importantly, there are many hubs located at the periphery of the network (large $k$, low $k_S$) that are poor spreaders.

2. For a fixed k—shell, $M(k_S,k)$ is approximately independent of the degree of the nodes.

   1. We see this in the vertically layered structure of $M(k_S,k)$, which suggests that infected nodes located in the same k—shell produce similar epidemic outbreaks, independent of the value of $k$ at the infection origin.

3. The most efficient spreaders are located in the inner core of the network (large $k_S$ region), fairly independently of their degree

"These results indicate that the k—shell index of a node is a better predictor [than degree ($k$)] of spreading influence. When an outbreak starts in the core of the network (large $k_S$) there exist many pathways through which a virus can infect the rest of the network; this result is valid regardless of the node degree."

"Similar results on the efficiency of high—$k_S$ nodes are obtained from the analysis of $M(k_S,C_B)$ in Fig. 2 (b,d,f,h), where $C_B$ is the betweenness centrality of a node in the network: the value of $C_B$ is not a good predictor for spreading efficiency."

k-shell structure

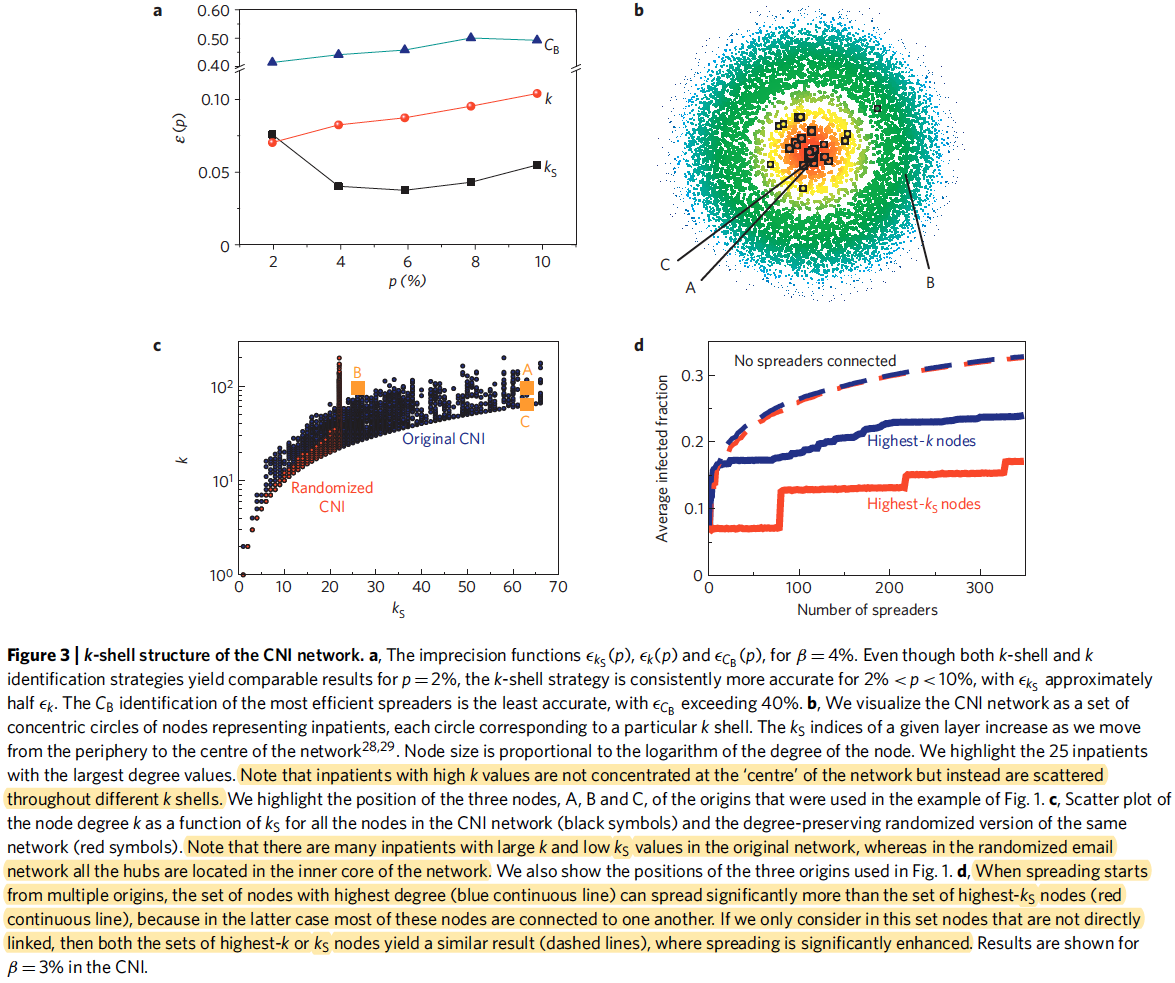
• See the original text for details on the "imprecision functions" covered in [Fig. 3a] — the general gist can be gathered from the figure description

• There are many hubs which exist in the periphery of a network [Fig. 3b] and therefore contribute poorly to spreading

  • This is a result of the rich topological structure of real-networks — in a fully randomized graph, all hubs are placed in the center of the network [Fig. 3c]

• If spreading starts in multiple locations, nodes with the highest degree can spread significantly more than the set of highest k-shell nodes. [Fig. 3d]

  • This is because high k-shell nodes are typically connected to one another

  • If we select only nodes that are not connected, we see that there is not much difference in the ability to spread and that, in both cases, this leads to the most efficient spreading process

    • "Clearly, the step-like features in the plot of highest-$k_S$ nodes (red solid curve in Fig. 3d) suggest that the infected percentage remains constant as long as the infected nodes belong in the same $k$ shell. Including just one node from a different $k$ shell results in a significantly increased spreading."

SIS Spreading

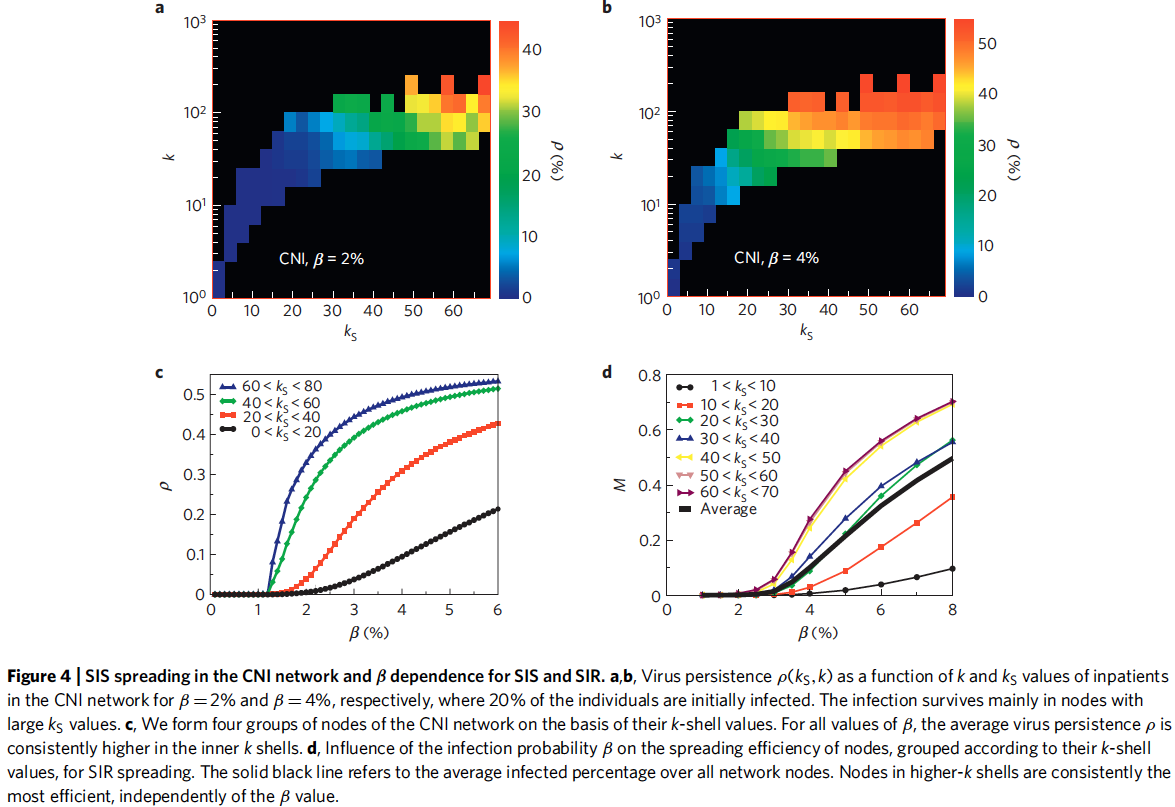
The spreading efficiency of a given node $i$ in SIS spreading is the persistence, $\rho_{i}(t)$, defined as the probability that node $i$ is infected at time $t$.

Previous studies have shown that the largest persistence is found in the network hubs.

"However, we find that this result holds only in randomized network structures. In the real network topologies studied here, we find that viruses persist mainly in high-$k_S$ layers instead, almost irrespectively of the degree of the nodes in the core." Fig. 4 a, b

• For all values of $\beta$ (spreading probability), the average virus persistence is consistently higher in the inner k shells. Fig. 4c
• Nodes in higher-k shells are consistently the most efficient at spreading infection, independent of the $\beta$ value (SIR model) Fig. 4d)

"Note that a virus cannot survive in the degree-preserving randomized version of the CNI network, owing to the absence of high-k shells. The importance of the inner-core nodes in spreading is not influenced by the infection probability values, $\beta$. In both models, SIS and SIR, we find that the persistence $\rho$ or the average infected fraction $M$, respectively, is systematically larger for nodes in inner $k$ shells compared with nodes in outer $k$ shells, over the entire $\beta$ range that we studied (Fig. 4c,d). Thus, the k-shell measure is a robust indicator for the spreading efficiency of a node."

Notes by Matthew R. DeVerna