Simulating dynamical features of escape panic

• Authors: Dirk Helbing, Illés Farkas & Tamás Vicsek
• Publication, Year: Nature, 2000
• Link to Paper

Contents

Summary

Lit Review

Model and Assumptions

Simulations

Potential Applications

Summary

• The authors develop a model for simulating escape panic in various situations
• Particularly important is the development of a single parameter $p_i$ which can be varied to simulate different levels of panic
• The model could be used to test the design of buildings and structures
• The authors call for quantitative data and video data to attempt to verify the simulated models with real world data.

Lit Review

• Panicking individuals tend to display maladaptive behavior such as "jamming" and life-threatening "over-crowding"

  • This has often been attributed to "social contagion"

• This observed jamming is a result of uncoordinated motion (aka "incoordination") and depends on the reward structure

• Drawing on "socio-psychological literature, reports in the media, available video materials, empirical investigations, and engineering handbooks" the authors list nine features of escape panic:

  1. People move or try to move considerably faster than normal.
  2. Individuals start pushing, and interactions among people become physical in nature.
  3. Moving and, in particular, passing of a bottleneck becomes uncoordinated.
  4. At exits, arching and clogging are observed.
  5. Jams build up.
  6. The physical interactions in the jammed crowd add up and cause dangerous pressures up to 4,450N $m^{-1}$ which can bend steel barriers or push down brick walls.
  7. Escape is further slowed by fallen or injured people acting as `obstacles'.
  8. People show a tendency towards mass behavior, that is, to do what other people do.
  9. Alternative exits are often overlooked or not efficiently used in escape situations.

These observations have encouraged us to model the collective phenomenon of escape panic in the framework of self-driven many particle systems

• Their simulations of crowd dynamics are based on a generalized force model

Model and Assumptions

• Assume a mix of socio-psychological and physical forces that influence the behavior of individuals in a crowd

Each of $N$ pedestrians $i$ of mass $m_i$ likes to move with a certain desired speed $v_{i}^{0}$ in a certain direction $e_{i}^{0}$, and therefore tends to correspondingly adapt his or her actual velocity $v_i$ with a certain characteristic time $\tau_{I}$.

Simultaneously, he or she tries to keep a velocity-dependent distance from other pedestrians $j$ and walk $W$.

This can be modeled by 'interaction forces' $\mathbf{f}_{ij}$ and $\mathbf{f}_{iW}$, respectively.

Mathematically, this is represented as...

…while the change of position $\mathbf{r}_i(t)$ is given by the velocity $\mathbf{v}_{i}(t) = d\mathbf{r}_i / dt$

• Additional equations are defined which describe the psychological tendency of two pedestrians to stay away from one another as well as their relationship to the walls — among some other model assumptions — these details are left out but can be found within the original text via the link at the top of the page.

• Generally, to minimize the number of parameters, for reasons of calibration and robustness, identical values were chosen for all pedestrians with one exception.

  • Some variation was needed to combat potential gridlocks from exactly balanced forces — to achieve this, the shoulder length of pedestrians was varied by uniformly distributing a diameter of $2r$ in the interval of [0.5m, 0.7m]

• With these model assumptions numerous escape panic phenomena are simulated...

Simulations

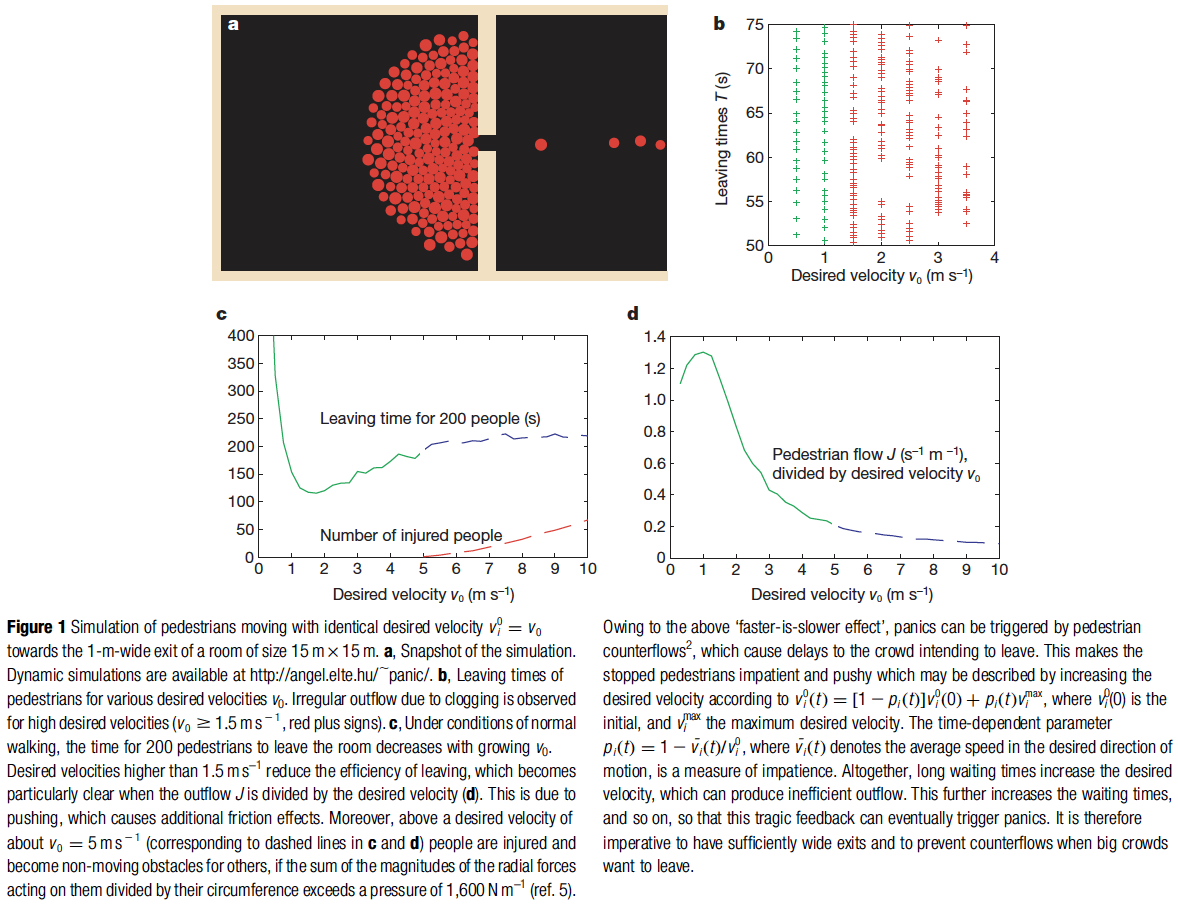
Transition to incoordination due to clogging (Fig. 1A & B)

• When the desired velocity $v_{i}^{0} >$ 1.5 m s$^{-1}$ — i.e. when people are rushing the simulation displays:

  • Arch-like blockings of the exit
  • Avalanche-like bunches of individuals exiting when the arches break

• This simulation is in parallel to empirical findings of real situations

'Faster-is-slower effect' due to impatience (Fig. 1c & d)

• As clogging the exit is connected to desired velocity, rushing also leads to a reduction in average speed of leaving if the friction parameter $k$ is big enough

What was learned

• The arching underlying the clogging effect at the exit requires a combination of two effects:

  1. Slowing down due to a bottleneck such as a door
  2. Strong inter-personal friction, which becomes dominant when pedestrians get too close to each other

• As a result, the dangers of clogging during a moment of panic can be reduced by avoiding bottlenecks in the construction of buildings, etc.

• Unfortunately, even for wide openings, some clogging effects can still be found (Fig. 2)

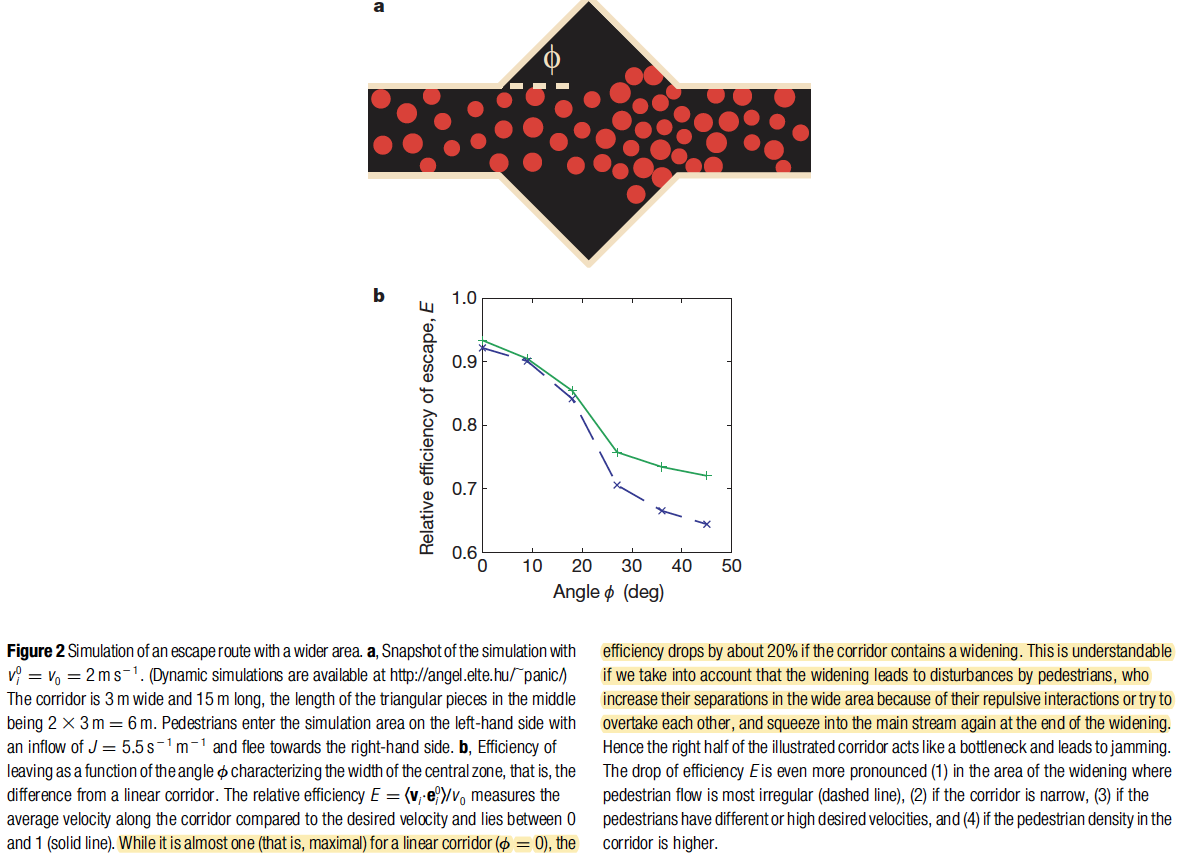
• What this shows us, basically is that — even if there is a very wide opening — if you have this angular widening effect shown in the triangular shapes that protrude from the hallway (fig 2a) a clogging effect will be the result. This is because people may try to overpass one another and then be "repulsed" outward into triangular area
• We can see that as the angle difference from the linear corridor ($\phi$) grows, the efficiency of escape is reduced.

Mass behavior

• They test a situation in which individuals would need to exit a smoky room but have to first find at least one invisible exit (Fig. 3)

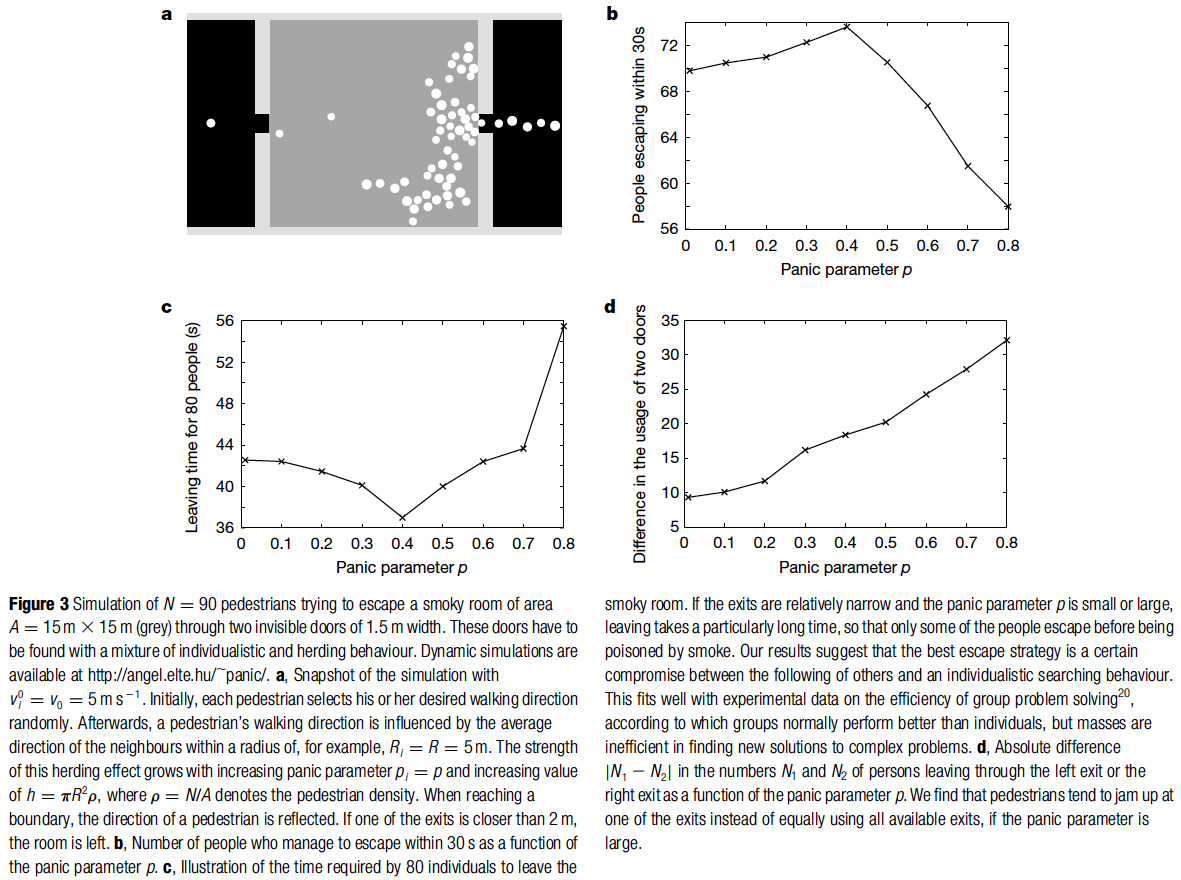
• In this simulation, each pedestrian $i$ can either choose an individual direction $e_i$ or follow the average direction $\langle e_{j}^{0}(t) \rangle$ of his neighbors $j$ in a certain radios $R_i$ — or try a mixture of both.

  • They assume both options are weighted by the parameter $p_i$ — which represents the degree of panic for individual $i$

… where $\text{Norm}(\mathbf{z}) = \mathbf{z} / ||\mathbf{z}||$ denotes normalization of a vector $\mathbf{z}$.

• What this means is...

  • When $p_i$ is high this means there is a lot of herding behavior
  • When $p_i$ is low this means that there is a lot of individualistic behavior

• What they learn is that that neither extreme is good

Pure individualistic behavior means that each pedestrian finds an exit only accidentally, while pure herding behavior implies that the entire crowd will eventually move into the same and probably blocked direction, so that available exists are not efficiently used (Fig. 3d), in agreement with observations. … we expect optimal chances of survival for a certain mixture of individualistic and herding behavior, where individualism allows some people to detect the exits and herding guarantees that successful solutions are imitated by the others.

Potential applications

• This model could be used to test buildings for their suitability in emergency situations.
• The single parameter $p_i$ is particularly useful for testing different levels of panic