The Computational Beauty of Nature

Info

• Authors: Gary William Flake

• Publication, Year: Book, 1998

  • Pages: pp. 1-8; 129-136

• Link to Paper

Contents

Introduction

• Simplicity and Complexity
• The Convergence of the Sciences
• The Silicon Laboratory

Post Script: Fractals

• Algorithmic Regularity as Simplicity
• Stochastic Irregularity as Simplicity
• Effective Complexity

Opening Quotes

The point of philosophy is to start with something so simple as not to seem worth stating, and to end with something so paradoxical that no one will believe it.

• Bertrand Russell

Things should be as simple as possible, but not simpler.

• Albert Einstein

Introduction

Reductionism: The idea that a system can be understood by examining the its individual parts

• Implicit in this idea is that you reduce the system into different levels i.e. understanding the parts of the parts, and the parts of those parts, etc

For example, biologists study living things at various levels ranging from the whole body, to organ systems, down to cellular structure. This can of course continue further down but its irrelevant here.

Eventually, we get to the subatomic particles called quarks and we are faced with a silly question:

Since everything ultimately breaks down to the quantum level, why aren't all scientists mathematicians at the core?

In this world, diagnosticians would analyze individuals at the level of the atom, which makes as much sense as building a home one particle at a time.

• At some point, reductionism is not useful for science

To put this another way, we can describe a duck in excruciating detail but we still do not truly understand a duck unless we see how it behaves in many contexts —> in the water, in the air, with other ducks, in relation to predators, etc.

Applying this perspective to the organization of science, we find at each level that there are two types of phenomena:

• Agents: molecules, particles, ducks, species
• Interactions of Agents: chemical reactions, immune system responses, duck mating, and evolution)

Studying agents in isolation is a fruitful way of discovering insights into the form and function of an agent, but doing so has some known limitations.

Reductionism fails when we try to use it in a reverse directions

Having a perfect understanding of how an agent behaves in no way guarantees that you will be able to predict how the single agent will behave for all time or in the context of other agents.

This leaves us with three options for analysis:

• Analyzing the sole agent —> Reductionism

• Analyzing how many agents form a global pattern

• Take an intermediate route by focusing on the interactions of agents

  • Sort of serves as the glue between these two different levels of analysis

     

Simplicity and Complexity

Complex systems can be described as those which given rise to emergent behavior.

• That is, systems which contain simple units that, when combined, form a more complex whole

Agents that exist on one level of understanding are often very different from agents on another level.

• Yet, surprisingly, the interactions on one level of understanding are often very similar to the interactions on other levels.

To understand why this might be we look at three attributes which can be used to describe the interaction of agents.

1. Collections, Multiplicity, and Parallelism:

   • Complex systems with emergent properties are often highly parallel collections of similar units

   • Parallel systems are inherently more efficient

   • Parallel systems which are redundant have fault tolerance - if an individual agent dies/fails at its duty, there are many others to continue the job

   • Subtle variations among the units of a parallel system allows for multiple problem solutions to be attempted simultaneously

     • You can think of a heard of gazelles try to avoid a lion. There are solutions to the problem of escape, and the social system of gazelles explores many options simultaneously. This guarantees the survival of the herd.

2. Iteration, Recursion, and Feedback:

   • For living things, iteration corresponds to reporoduction

   • Iteration involves a form of persistence in time (where as parallelism lives in space)

   • Recursion is responsible for the various types of self-similarity seen in nature

   • Systems are often recurrently tied to their environment through feedback mechanisms

     • That is, animals can react to and change their environment. This means that future animals will have to take these environmental changes into account, for better or worse.

3. Adaptation, Learning, and Evolution:

   • Adaptation can be viewed as a consequence of parallelism and iteration in a competitive environment with finite resources

     • Thus, the combination of multiplicity and iteration acts as a sort of filter - i.e. natural selection

   • With feedback mechanisms in place b/w agent and environment, adaptation forms a "loop" in the cause and effect of changes in both agents and environments

There are, of course, many other ways to describe the agents and agent interactions. However, these do a good job of describe many aspects of how agents interact. Importantly, multiplicity, iteration, and adaption are universal concepts in that they are apparently important attributes for agents at all levels — from chemical reactants to biological ecosystems.

Describing Interactions b/w Agents

This task is typically quite difficult because we need to consider the entire environment in which the agents exit

The simplest type of question we can ask is, "What will $X$ do next, in the presence of $Y$?"

• Notice the difference between this question — which basically translates to, "What will $X$ do?" — and is very different from a more standard reductionist question, "What is $X$?"

   

The Convergence of the Sciences

Scientists' areas of expertise have become so specialized that communication among scientists who are allegedly in the same field has become difficult, if not impossible.

• This is typically worse for the older sciences like physics and biology

You also have scientists falling into the groups of "theorist" and "experimentalist"

• Most scientists do not dabble in both areas

A recent renaissance in science has largely come about thanks to computers

• Computers have blurred the lines between theoretical work and experimental work making both much easier
• Someone who creates and uses a simulation is simultaneously engaging in theory and experimentation

What types of simulations have been built?

• Meteorologists build weather simulations
• Physicists study the flow of plasma and the annealing of metals
• Economists have modeled various types of economies
• Psychologists have examined cognitive models of the brain

In all cases, scientists have found beauty and elegance in modeling systems that consist of simple, parallel, iterative, and/or adaptive elements. More important, scientists have been making discoveries that have been relevant to multiple fields. Thus, in many ways, the computer has reversed the trend toward fragmentation and has helped the sciences converge to a common point.

The Silicon Laboratory

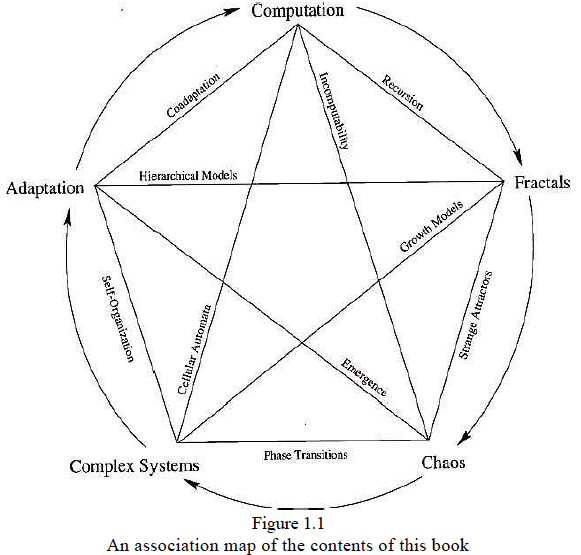
The book covered five major parts. The first part is the general introduction and the remaining four are what Flake considers to be the four most interesting computational topics of today:

1. Fractals — beautiful images which can be efficiently produces by iterating equations. Since they can be computationally described, it is interesting to see that they are often found in natural systems. I.e. the growth of trees or the branching of bronchial tubes in human lungs

2. Chaos — A special type of fractal, known as strange attractors are often associated with Chaos. Chaos makes the future behavior of deterministic systems such as weather, economies, and biological systems impossible to predict in the long term but predictable in the short term.

   • Chaos can often be found when nonlinear systems are iterated repeatedly
   • Also found in multi-agent complex system such as and social structures

3. Complex systems — Complex systems consist of many very simple units that interact. The amount of interactions among agents partially determines the degree of the systems chaos. One extreme has very little interaction, this leads to static patterns. On the other end, we have intense interaction which can boils down to complete chaos.

4. Adaptation — Adaptation allows for complex systems to change adapt, learn, and evolve. You can think of evolutionary systems, classifier systems, and artificial networks. Genetic algorithms, for example, can be used to evolve solutions to a wide variety of problems.

The connections between them are depicted in the figure below.

Post Script: Fractals

It is indeed a surprising and fortunate fact that nature can be expressed by relatively low order mathematical functions.

— Rudolf Carnap

Everything you've learned in school as "obvious" becomes less and less obvious as you begin to study the universe. For example, there are no solids in the universe. There's not even a suggestion of a solid. There are no absolute continuums. There are no surfaces. There are no straight lines.

— R. Buckminster Fuller

Mathematics is the science of patterns.

— Lynn Arthur Steen

Flake provides an analogy of fractals to computer programs.

Computer programs have a "dual- identity that is an artifact of a trade-off between time and space."

• The stored computer program can be thought of as a compact recipe for distinguishing between numbers that do and do not belong in a set —> "all prime numbers that are one less than a perfect power of 2"
• However, to actually enumerate this set would require an infinite amount of time to "unwind" the set.

Hence, while the verbal description is finite in length but requires infinite time to "unwind," the enumerated set requires infinite space to store it but exists independently of time.

He then claims that fractals, both deterministic fractals and stochastic fractals, come from special types of programs that exhibit the same duality.

• Natural fractals are often so structurally elaborate that they can't be described with classical geometry.

  • However, their form will have a simple functional cause. For example, for biological systems this cause is usually related to parallel growth processes that have competing goals — i.e. a need for surface area vs. maximizing building material (think of the folds in a brain)
  • For random (stochastic) fractals, however, there is typically a simple, single, parallel process that occurs multiple spatial scales — i.e. erosion

Thus, the structural recursion of a fractal will always be related to a functional recursion that takes place in the creation of the natural fractal.

Algorithmic Regularity as Simplicity

Simplicity: things that can be compressed are simpler than things that cannot be compressed

The formal study of how things can be algorithmically compressed is know as Algorithmic Complexity (AC) or Kolmogorov Complexity (named after Andrei Kolmogorov, an early pioneer of the field)

• Time Complexity: the amount of time that it takes to compute a function for some particular input length
• Space Complexity: characterizes the amount of computer memory that an algorithm will need at any time during is execution

In AC, the central issue is the required length of a program to produce a set of numbers of symbols

For example, you can store the set of numbers from 0 through $N$ by writing all of them out by hand. Or you can write them with Python code like the below.

1
(print(i) for i in range(N))

• The only restriction that is placed on programs of this nature is that they must take no input

Thus, if we wanted to write this for the limit of 1000, we would write

xxxxxxxxxx
1
1
(print(i) for i in range(1000))

As a result, the length of this program will always grow proportionally to

Note: the big $O$ above is simply a notation style that is used to classify algorithms according to how their run time or space requirements grow as the input size grows. This builds on the mathematical notation which describes the limiting behavior of a function when the arguments tend towards a particular value or infinity — also knows as asymptotic notation (for obvious reasons). See the wikipedia page for more details on "Big O notation". 😄 ​

This makes sense because the only thing that changes in the above equation is the length of the input $N$.

Going back to time vs. space — AC tells us exactly how much one can be traded for the other

• For example if you can't actually store a large set of number in the computer's memory — AC can show us that a portion of the space in memory can be replaced with computational time if we were willing to sacrifice that some of the set would need to be reconstructed on the fly.

This then formalizes what it means for a set of numbers to be compressible and incompressible

• Compressible = redundant, patterned, contain relatively little information
• Incompressible = random, without pattern

Stochastic Irregularity as Simplicity

Algorithmic complexity is limited in that it is not very intuitive. One example of this has to do with randomness vs complexity. In fact, while AC considers randomness to be complex, some forms of randomness can actually be considered quite simple.

• For example, we can think of a simple stochastic Gaussian function like flipping a fair coin. While the process at the most base level is unpredictable because it's unclear whether you will flip a head or tail — over the long run the process is actually quite easily predictable, forming a simple bell curve.

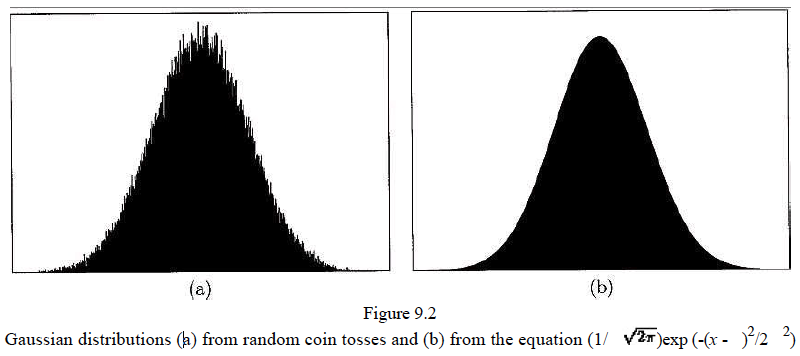
Given a gaussian function, all we need is the mean and standard deviation to describe the entire systems behavior.

Thus, random processes are also compressible because many instances can be described by a small collection of numbers. So even though any particular coin toss is unpredictable, the properties of collections of coin tosses are very predictable.

As an analogy, it is impossible to keep track of the trajectories of individual molecules in a closed volume of air, since there are simply too many ways that gas molecules can collide with each other. Nevertheless, collections of gas molecules behave in very predictable ways. Knowing only the temperature and pressure of a gas tells you enough about the whole ensemble of molecules that you can effectively ignore what the individual molecules are doing. Notice that the properties of temperature and pressure cannot be attributed to a single gas molecule but only to collections of molecules. Similarly, the mean and standard deviation of a normal random process make sense only for collections of random events. Yet these two numbers manage to get to the essence of what is important about a particular normal distribution.

Effective Complexity

What we have now, is a contradiction between these two perspectives of complexity vs. simplicity? So how to we resolve this?

To address this, folks like James Crutchfield, Charles Bennet, Murray GellMann, David Wolpert , and William Macready have been working on the concept of "effective complexity".

• Effective complexity:

  • Simple things = things that are strictly regular as well as strictly irregular
  • Complex things = things that are neither regular nor irregular

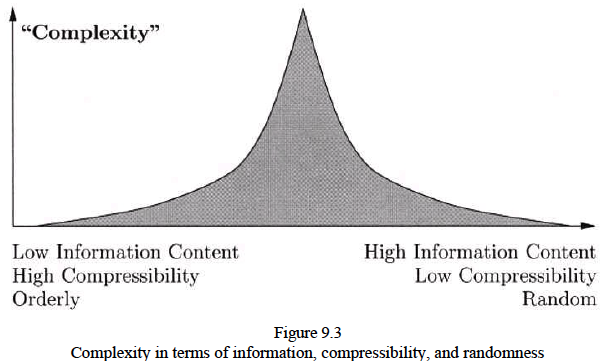
Ends of the spectrum

• Left: Pure regularity that can be found in Euclidean objects such as a simple set of numbers

• Right: Pure noise. Like a random coin flip.

  • Brownian motion would be slightly more complex because Brownian processes must have "memory"

  • For example, every new random number is always "selected" relative to the previous number. As a result, this is not a truly random set of numbers, but a set of numbers which are each the sum of the previously selected number.

    • This added interaction between the agents within the system creates complexity because a completely random noise can be described simply like a Gaussian function, however, the reliance on the previously chosen number makes the Brownian noise a bit more difficult to predict.

Where do fractals fall on this spectrum?

• Fractals are considered complex. While these objects can often be easily described by some iterative function/program, they must run forever in order to capture the infinite self-similarity that they contain.

  • Remember that, from the AC point of view, complexity takes into account time and space

• Thus, fractals are on the "edge of complexity" because they can be compactly described but can only be realized by "programs" that never stop

At the very peak of complexity, we would hope to find things such as the human brain, but this is just speculation on my part.

Notes by: Matthew R. DeVerna