Revisiting the Foundations of Network Analysis

Authors: Carter T. Butts

Publication, Year: Science, 2009

Link to Paper

Notes by: Matthew R. DeVerna

Intro

• Network science has exploded into many different fields

• The knowledge gained from this explosion is obviously good, however, we need to be careful to make sure that everyone is using a standardized approach

  • If we don't, this expansion of network science may lead to inappropriate conclusions and generally poor results

Standard Framework and Core Assumptions

• Most network research is borrowed from graph theory

• Terms:

  • Nodes = single entity

  • Edges = relationships between notes

    • Edges are either:

      • Unordered pairs —> relation is said to be undirected
      • Order pairs —> relation is said to be directed

  • Degree centralization = a measure of the extent to which ties are concentrated on a small number of nodes

• This can be extremely restrictive because we must be able to reduce a system to a well-defined set of discrete components whose interactions are strictly dyadic in nature.

  • For any given pair of components (nodes) the relationship is dichotomous in that it either exists or does not
  • While this may be restrictive, it is often used an approximation to the structure of a more complex system, in order to study a particular property of that system — i.e. how a disease spreads in a community over time

• In fact, this reductive nature of the graphical approach is what has allowed its mathematical development and scientific advances

• Extensions of this basic framework are many and varied — this allows for more complex analyses

  • Edges can carry different weights
  • Multi-lateral relationships (i.e. group memberships) can be represented as "hyperedges"
  • Temporal aspects can be handled by treating them as time series data — i.e. with repeated cross-sectional sampling of group structure

Many measurement, analysis, and modeling techniques are rooted within the standard framework. However, when assumptions of this framework do not serve as reasonable approximations of the system of interest, alternative representations and techniques may be necessary. What factors should be considered when choosing a network representation, and what are the consequences when this choose is poorly made?

When is a Node a Node?

• When extending the basic assumptions described above one could, for example, define a certain "class" of entity.

  • Doing so assumes that:

    1. This class can be clearly defined
    2. Grouping entities in this class will be scientifically useful

  • Using individual humans as nodes in a study of, friendship, kinship, and the individual use of publications in citation studies are examples where this assumption is well-justified.

  • However, study's which aggregate this groups as, for example, households, or organizations, may encounter problems due to the fluidity of the interacting units and the fact that subunits of a larger unit may themselves interact with others both within and without the "parent"

  • Grouping smaller entities into larger groups can obscure the difference between smaller units and may incorrectly suggest that these entities are equal in all ways

• Changing the node set can substantially influence the size and density of the resulting network, with considerable implications for subsequent analysis

  • Degree centralization is one which is qualitatively and quantitatively changed based on the size of the network (even for relatively simple models)

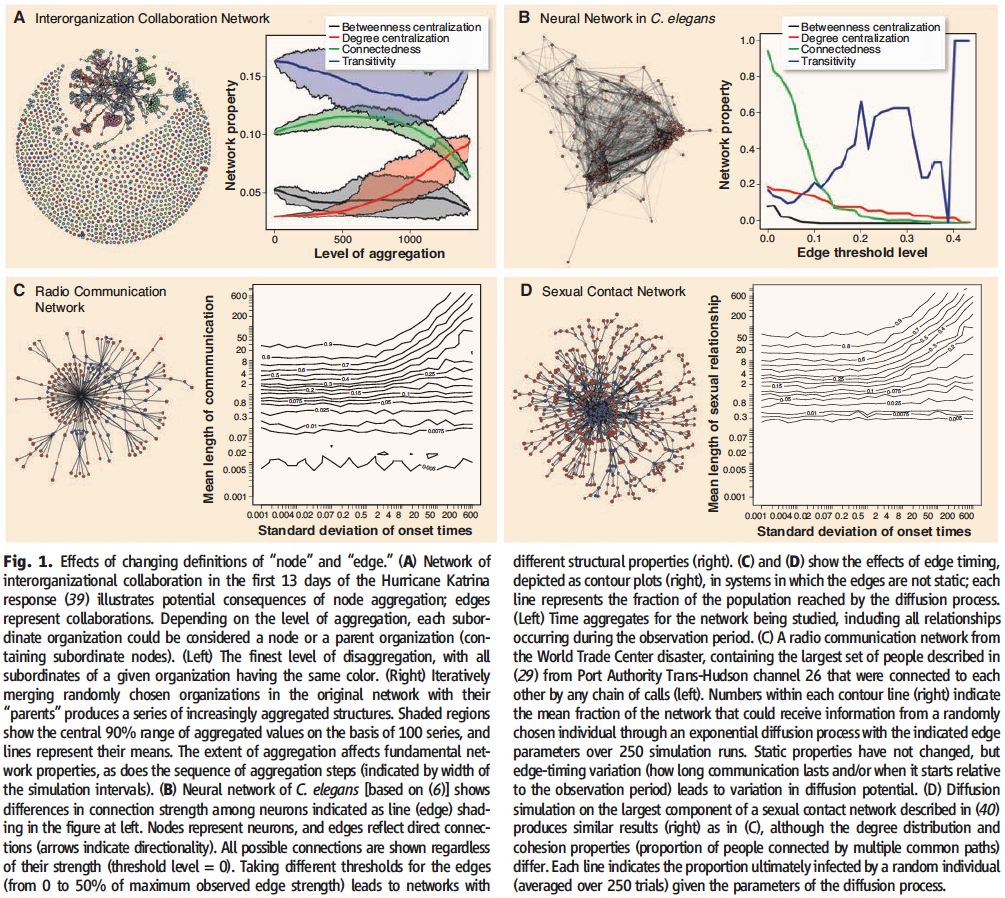
• In hierarchal contexts, different aggregation decisions can produce networks with very different structural features (Fig 1A)

To avoid misleading conclusions, the set of nodes should be defined so as to include all distinct entities that are capable of participating in the relationship under study; this definition should be used consistently across networks. Where no such set of entities can be uniquely identified, it is possible that a finite network representation will be inappropriate. An alternative framework (such as a continuous spatial representation) may prove more fruitful. In other cases [such as multilevel processes], simultaneous analysis of the same system at multiple levels of aggregation may be appropriate.

When is an Edge an Edge?

• Even for relations with quantitative aspects, one can often usefully identify relationship as present or not present

• When a relationship reflects an interaction, the use of a binary representation can greatly simplify both theory and measurement

• However, dichotomous distinctions can sometimes be misleading.

  • For example, many interactions are inherently episodic and occur at variable rates

  • Dichotomizing this type of data can hide these variations but also requires selecting a threshold level of some kind

    • This choice can lead to substantially different network properties within the resulting network both through

      1. Selective tie removal (directly)
      2. Changes in network density (indirectly)

    • The range of structures present at different connection strengths can vary greatly (Fig 1b)

This cannot be resolved solely with better data collection or more elaborate statistical techniques. Rather, one must determine whether the relationship under study is sufficiently stable to be well-approximated by a constant function over the period of interest and whether the values taken by this function across pairs are sufficiently constrained to be approximately dichotomous.

• For highly heterogenous relationships (i.e. trade or migration rates) no single threshold may suffice

  • It's usually more appropriate to use a weighted graphical representation

Time Scales and Network Processes

• When considering representation of nodes and edges, it is crucial to also consider the time scale on which the processes of study unfold

  • For example, studying information diffusion — which often occurs over the course of hours or days — utilizing stable relationships like kinship or friendship — which have turnover rates on the order of years — it is reasonable to consider these connections as stable/static

• Failure to consider how these dynamics may change over time — whatever the temporal scale may be — can create extremely misleading results.

The timing and duration of relationships are critical factors in the susceptibility of the dynamic network to disease transmission, factors that are hidden by the time-aggregated representation. This can be seen in Fig. 1D; for a given network, everyone may become infected or no one may be infected, depending on the edge duration and time of onset.

Conclusion

To represent an empirical phenomenon as a network is a theoretical act. It commits one to assumptions about what is interaction, the nature of that interaction, and the time scale on which that interaction takes place. Such assumptions are not "free," and indeed they can be wrong. Whether studying protein interactions, sexual networks, or computer systems, the appropriate choice of representation is key to getting the correct results.