Emergence of Scaling in Random Networks

• Authors: Albert-Lászlo Barabási, Réka Albert
• Publication, Year: Science, 1999
• Link to Paper

Summary

This is a classic network science paper which paved the road for the field. In this paper the authors highlight two properties of real networks which give rise to (and are necessary for) the emergence of scale-free properties: growth and preferential attachment.

Scale Free Networks in the Wild

The authors begin by highlighting three real-world networks which display scale-free properties — that is a network in which the degree distribution follows a power-law.

1. Collaboration network of movie actors

   • Nodes are actors, and the edges represent co-starring in a moving

2. The World Wide Web

   • Nodes are webpages, and edges are links points from one page to another

3. Electrical power grid of the western United States

   • Nodes are generators, transformers, and substations — edges are the high-voltage transmission lines

Each of these network's degree distributions follow a power law. That is...

… independent of the system and the identity of its constituents, the probability $P(k)$ that a vertex in the network interacts with $k$ other vertices decays as a power law, following

… which implies that these networks self-organize into this scale-free state — which was not predicted by existing models at the time.

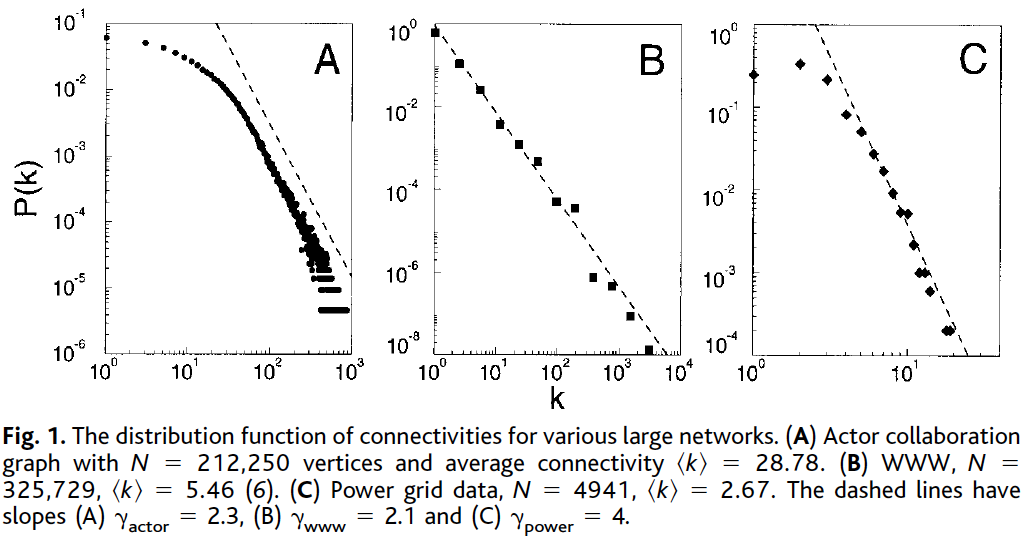
• Image Credit: Emergence of Scaling in Random Networks

Comparing to Random Graph (Erdös Rényi) and Small World Models (Watts Strogatz)

Basically, these models overlooked the two factors that drive the scale-free network properties.

1. Growth — these networks will continue to get larger over time.
2. Preferential attachment — the fact that higher-degree nodes may be more valuable/attractive and that new nodes are more likely to attach to these high-degree nodes.

The random graph model assumes the probability that a node will have $k$ edges follows a Poisson distribution.

The small world model assumes $N$ nodes form a lattice where each node is connected to its two nearest and next-nearest neighbors. Additionally, with a probability of $p$ each node is the connected to another node chosen at random.

… both models assume that we start with a fixed number ($N$) of vertices that are then randomly connected (ER model), or reconnected (WS model), without modifying $N$. In contrast, most real world networks are open and they form by the continuous addition of new vertices to the system, thus the number of vertices $N$ increases throughout the lifetime of the network.

• Image Credit: Collective dynamics of ‘small-world’ networks, Watts & Strogatz (1998)

~~

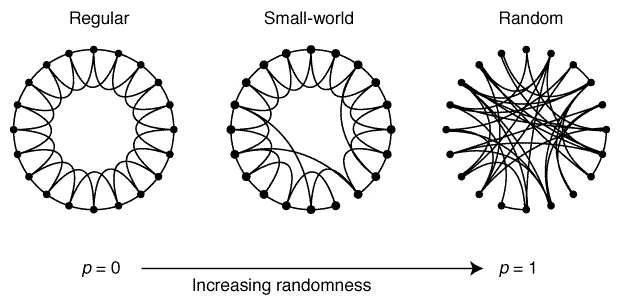
The authors also go through a modeling procedure to illustrate that the above two network features are necessary for the power law distribution to emerge. I am leaving this detail out for brevity's sake. Feel free to reference the original paper for these details.

Notes by Matthew R. DeVerna